RC直列回路の挙動

RC

＃1微分方程式を解く　変数分離型

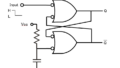
回路図は、

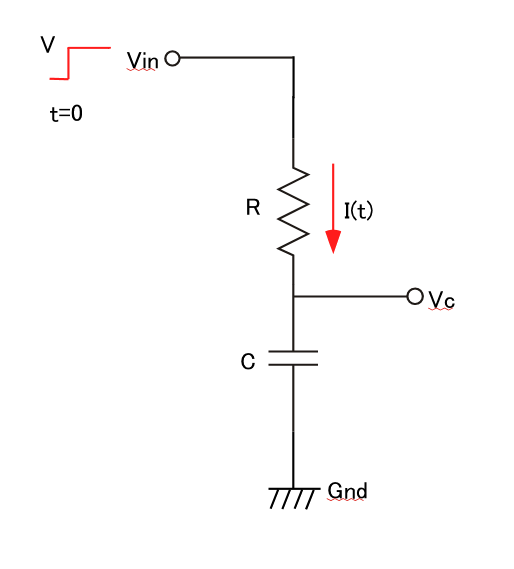
このように抵抗RとコンデンサCを直列につないで、上図Vinにt=0のタイミングで一定電圧Vを加えた場合のコンデンサの電圧変化を調べようということです。図のように回路に流れる電流の時刻tの時の電流値をI(t)とすると、定常的に抵抗Rの両端電圧Vr=I(t)R、コンデンサCの両端電圧は、コンデンサに蓄えられている電荷Q=CVcとすると

V=i(t)R+QC\large V = i(t)R + \frac{Q}{C}

の関係が成り立つ、今

Q=∫0ti(t)dt\large Q=\int^t_0 i(t) dt

なので、

V=i(t)R+1c∫0ti(t)dt\large V=i(t)R + \frac{1}{c}\int^t_0i(t)dt

となる。両辺をtで微分すると、左辺は定数なのでゼロ。従って、

0=1ct+Rdidt\large0 = \frac{1}{c}\,t + R\,\frac{di}{dt}
Rdidt=−1Ci\large R\,\frac{di}{dt} = -\,\frac{1}{C}\,i

整理して、

1idi=−1RCdt\large \frac{1}{i}\,di = -\,\frac{1}{RC}\,dt

両辺を積分するつまり∫\intをつけるだけ。

∫1idi=−1RC∫dt\large \int\frac{1}{i}\,di = -\frac{1}{RC}\int\,dt

結果

log⁡i=−1RCt\large\log\,i = -\,\frac{1}{RC}\,t

つまり、

i=Ae−1RCt\large i = Ae^{-\,\frac{1}{RC}t}

ただしAは積分定数で、初期条件t=0の時にVc=0とみなせるので、A=VRA = \frac{V}{R}　である。

結局

i=VRe−1RCt\large i = \frac{V}{R}\,\large e^{-\,\frac{1}{RC}\,t}

時刻tの時のVcは、

Vc=V(1−e−1RCt)Vc = V(1-e^-\frac{1}{RC}\,t)

となる。具体的に数値を与えてグラフを描いてみよう。

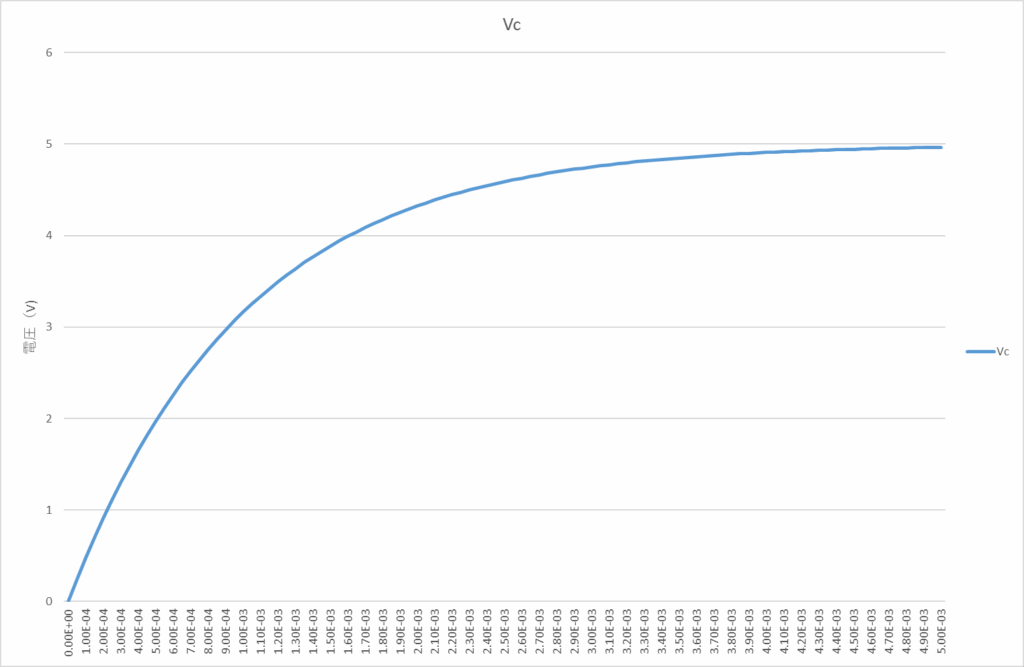
このようになる。今Vin=5V,R=1kΩ,C=1μFとした。上図のVcの増加はVinに漸近するが、その立ち上がりの速さは、RCで決まる。RCの単位は秒で、その値は1ｍｓである。このRCの積を時定数と呼ぶ。RCの単位が秒[s]になるのは、

R=VI=[V][A]R = \frac{V}{I} = \frac{[V]}{[A]}
C=QC=[A][t][V]C = \frac{Q}{C} = \frac{[A][t]}{[V]}

よって、RCの次元（単位ともいふ）は、

RC=[V][A][A][t][V]=[t]RC = \frac{[V]}{[A]} \frac{[A][t]}{[V]} = [t]

の通りである。

今知りたいのは、Vcが1.4Vほどになる時刻tである。グラフから概略の値は横軸の表示が読み取りにくいので不明。Excelで数値計算してるので、テーブルで確認すると、

	6	3.00E-04	0.740818221	0.259181779	1.295908897					
	7	3.50E-04	0.70468809	0.29531191	1.476559551					
	8	4.00E-04	0.670320046	0.329679954	1.64839977

ということで、300μsより大で、350μsより少ないという程度と分かる。正確な値は、Vcの式をtについて解いて計算すればよい、

t=−RClog⁡(1−VcV)t = -RC\log(1-\frac{Vc}{V})

において、R=1000,C=1.00E-06,Vc=1.4,V=5を入れて、


Desmos | 関数電卓

で計算すると、

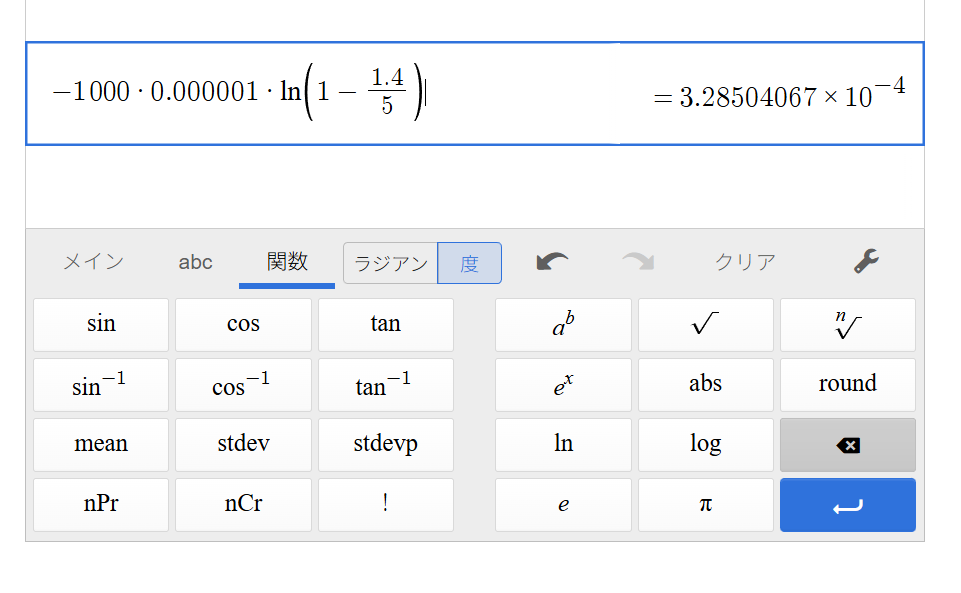
となるので、328μsという答えが得られた。具体的な電圧値1.4VというのはTTL Logic ICにおけるL->Hの遷移電圧である。これが具体的に意味を持つ回路を次の記事で紹介する。

コメント