RC回路の解析

まじめに微分方程式を解く

最後になってしまいましたが、4端子回路のローパスフィルターの回路方程式（微分方程式）を解いてみましょう。いけるところまで行ってみます。回路は、

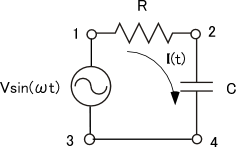
と書けますね。時刻ｔにおける回路を流れる電流の値をI(t)としています。一応図の矢印の向きが＋として、逆方向に流れる場合を-としましょうか。ωは角振動数です。さて、I(t)に関して、

\large Vsin(\omega t) = RI(t) + \frac{1}{C} \int I(t)dt　\tag 1

が成り立ちます。実験＝実測である、

の典型的な結果である、

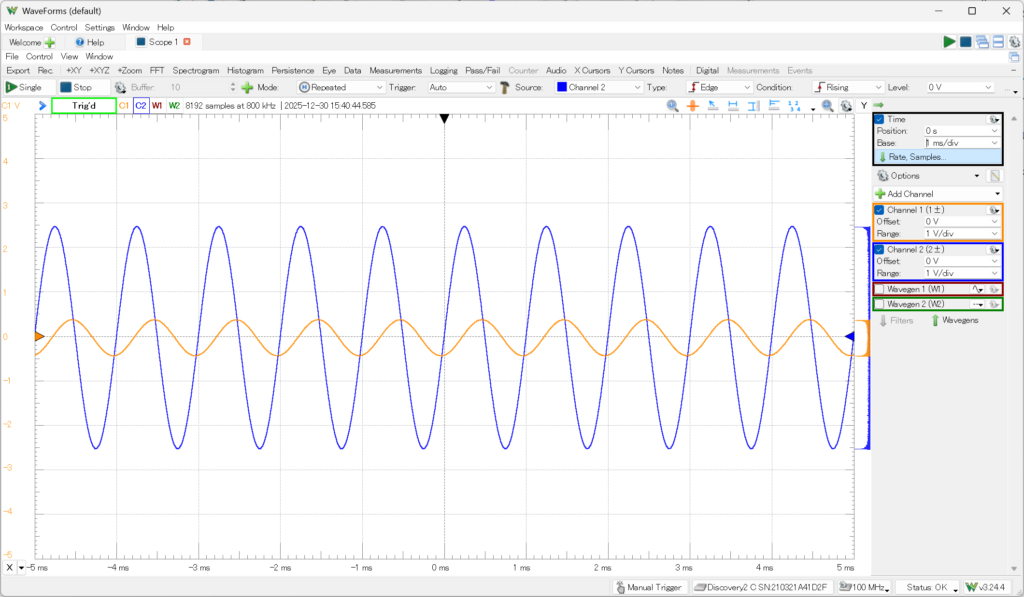
これから、

\large I = I_0 \sin(\omega t + \theta)

と置けることが予想されます。これを式（1）に入れると、右辺は、

\large R I_0\sin(\omega t + \theta) -I_0\frac{1}{\omega C}\cos(\omega t + \theta)

となり、

\large A\sin\alpha + B\cos \alpha　= \sqrt {A^2 + B^2}\sin(\alpha+\beta)

\large \cos \beta = \frac{A}{\sqrt{A^2+B^2}} \,\,,\sin\beta = \frac{B}{\sqrt{A^2+B^2}}

の形とみなすと合成の公式が適応できます。ごちゃごちゃ計算すると、最終的に

右辺は、

\large I_0 = \frac{V_0}{\sqrt{R^2+(\frac{1}{\omega C})^2}}\,\,

となり、

\sqrt{R^2+(\frac{1}{\omega C})^2}

が交流回路での周波数ωの時点での抵抗分（インピーダンスといったりリアクタンスといったりします）を表していることになります。この量自体が周波数（ω）に依存していますが、今問題はゲインの周波数依存性を調べたいので、コンデンサの両端の分圧分は、

\large \frac{\frac{1}{\omega C}}{\sqrt{R^2+(\frac{1}{\omega C})^2}}\,\,

これがローパスフィルターのゲインです。これをExcelで計算して、プロットしてみましょう。

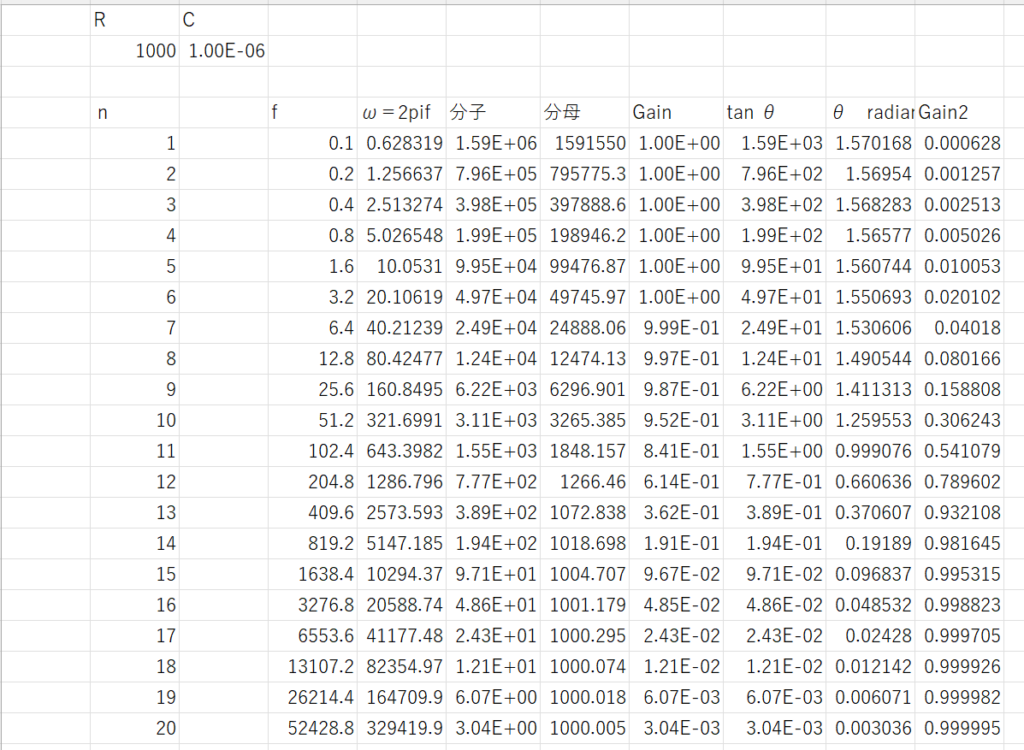
このような数表を作ってから、グラフ化すると、

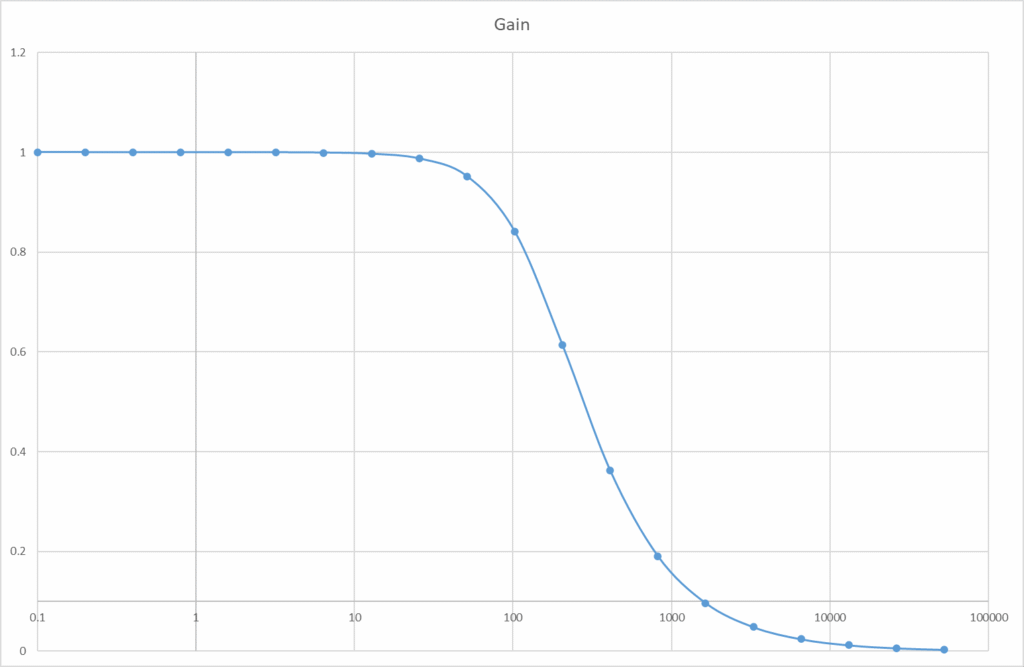
横軸は対数目盛ですが、nが変数ですからfじゃないです。形はらしいですね。Rの両端電圧は、

\large \frac{R}{\sqrt{R^2+(\frac{1}{\omega C})^2}}\,\,

なのでついでに計算しています。そちらをプロットすると、

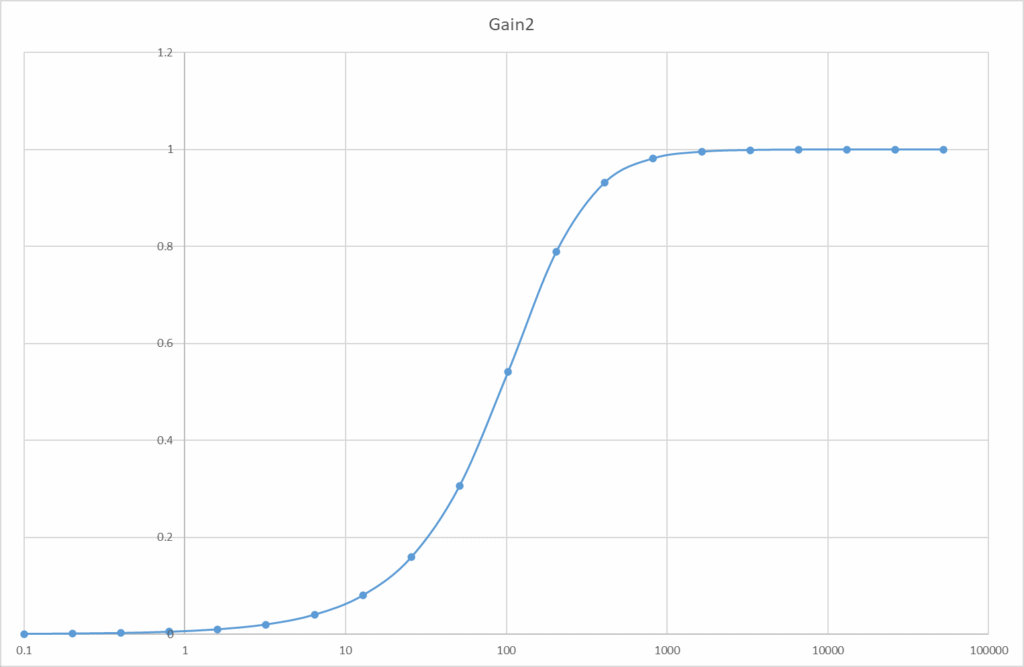
ハイパスフィルターの特性が見えています。位相差の導出はここでは触れませんけど、

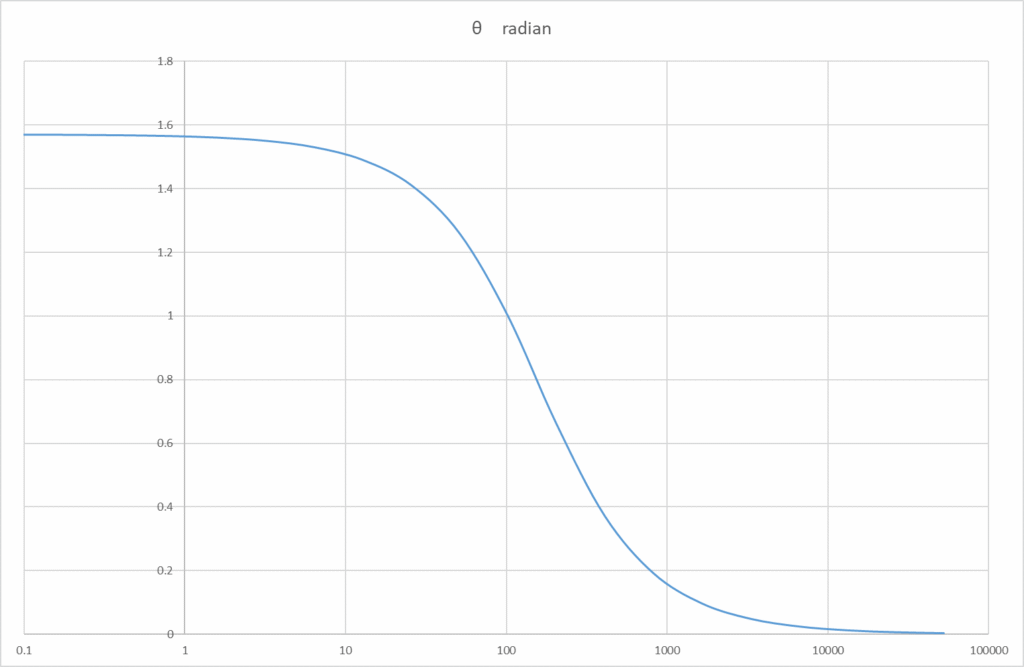
と求められました。これはローパスフィルターの場合です。