Analog Discovery 2を使う場合に留意する点

ADコンバーターの分解能

Analog Discovery 2で波形を観察している時は、ADC(AD変換器）を使ってデータを集めて、それをfancyに表示しているわけですが、このADCのスペックを示しておきましょう。

入力チャネル数： 2CH
周波数帯域： 30MHz
サンプリング周波数： 100Msps
分解能： 14bit

ということになりますが、この記事で着目するのは分解能のところです。14bitですね。Analogな物理量（普通は電圧）をAD変換しますから、その結果が最大で14bitで表現されるわけです。有限の分解能ですから、当然量子化誤差（Quantum Error)が発生します。よく±1/2LSBと表現されますが、その物理的意味を考えます。横軸に現実世界の物理量（電圧、電流、重さなどの連続量）を取り、縦軸にそれを入力としてAD変換した結果を表すと、入出力の関係は階段状のグラフになります。郵便料金をはじめとする公共料金での使用量と支払い金額の関係もこのような階段のグラフになります。今簡単のために8bitのADCの場合を示すと、

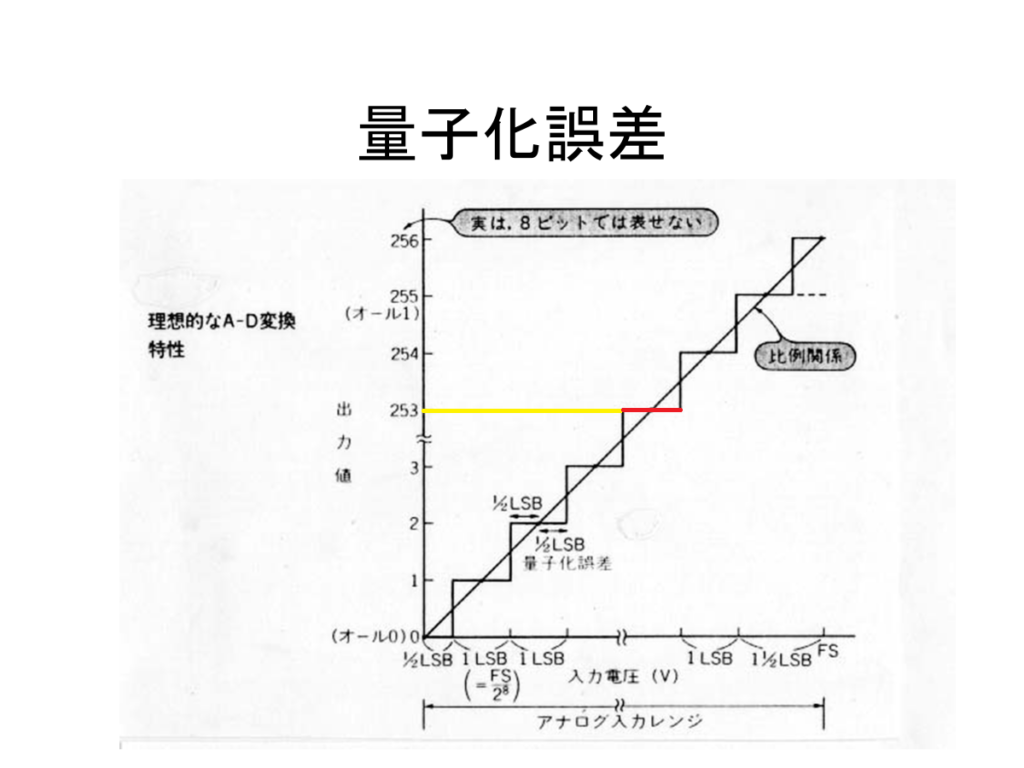
のようになります。今上図のように出力値（AD変換で得られた結果）が253だったとすると、それに対応する入力電圧範囲は幅を持っていて、上図の赤で示した領域に該当します。この範囲の入力電圧は全部253に変換されます。従って、±1／2LSBの誤差を含みます。LSBとはLeast Significant Bitの頭を取ったもので、フルスケール（0～255）を $2^8$
で割ったものです。

さて実験や計測をしていると普通は有効数字は3桁ということになりますが、一体何bitのADCを使えばこの精度が得られるかを概算しておきましょう。有効数字3桁ということは、0.001が分解できればいいのですが、2のべき乗を計算していき1000を超えたところでその数字を求めればよいですね。

\large 2^{10} = 1024 > 1000

なので、10bit以上のADCを使えば良いということがわかります。現実にはbit数は、4の倍数になっていることが多いので、12bitのADCを使うことになります。Analog Discovery 2は分解能としては十分ですね。ただしこれは必要とされるADCの分解能なので、もう一つの重要なパラメーターであるサンプリング周波数については、別記事で書きます。

余談ですが、上式を