RCの回路実験

正弦波を食わせてみよう

ローパスフィルターとしての特性を調べてみよう

前記事

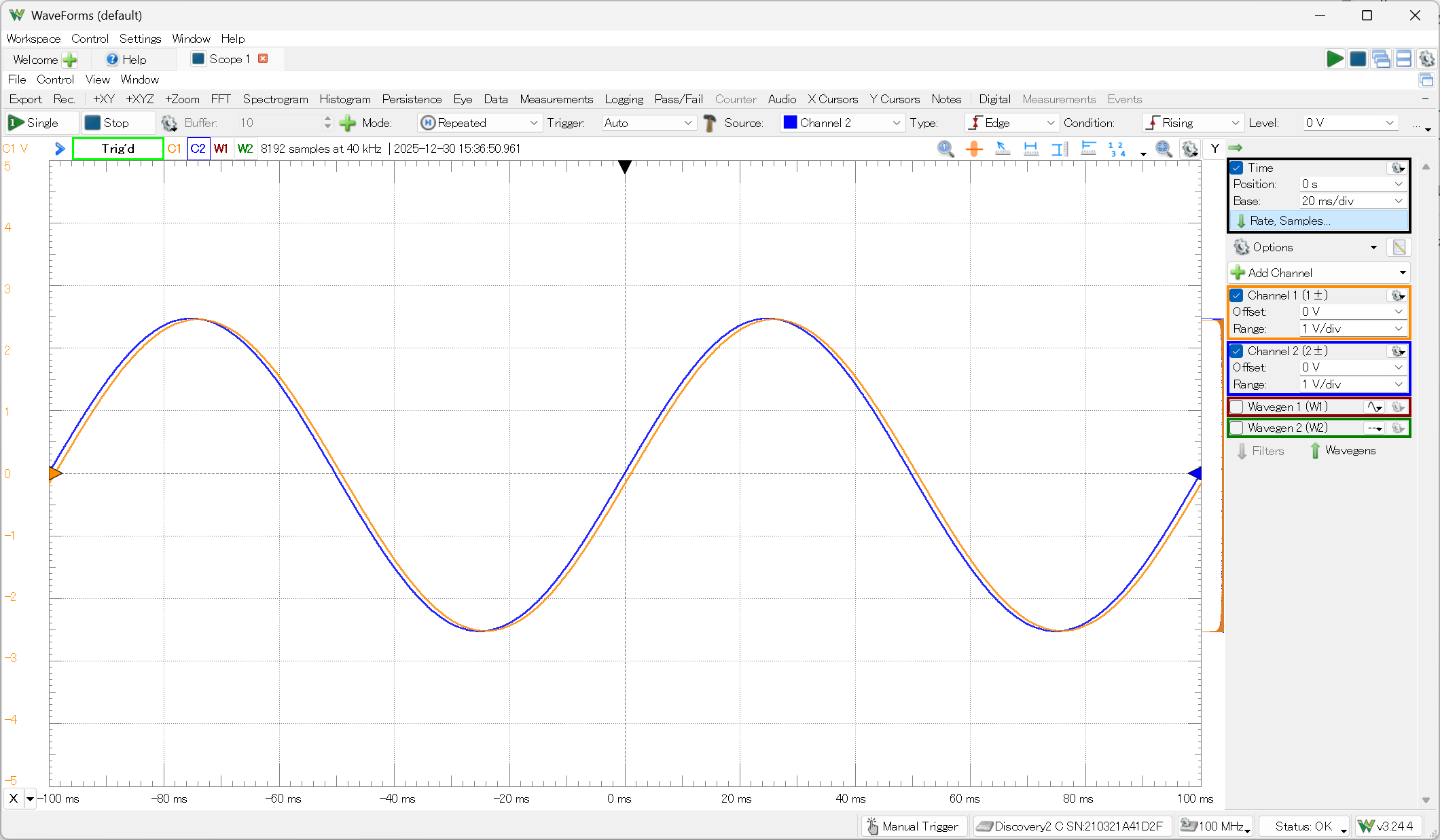
で矩形波の入力時の応答を検分したが、今度は色々な周波数の正弦波を入れた場合の出力（正弦波）の振幅や位相がどうなるかを調べてみよう。

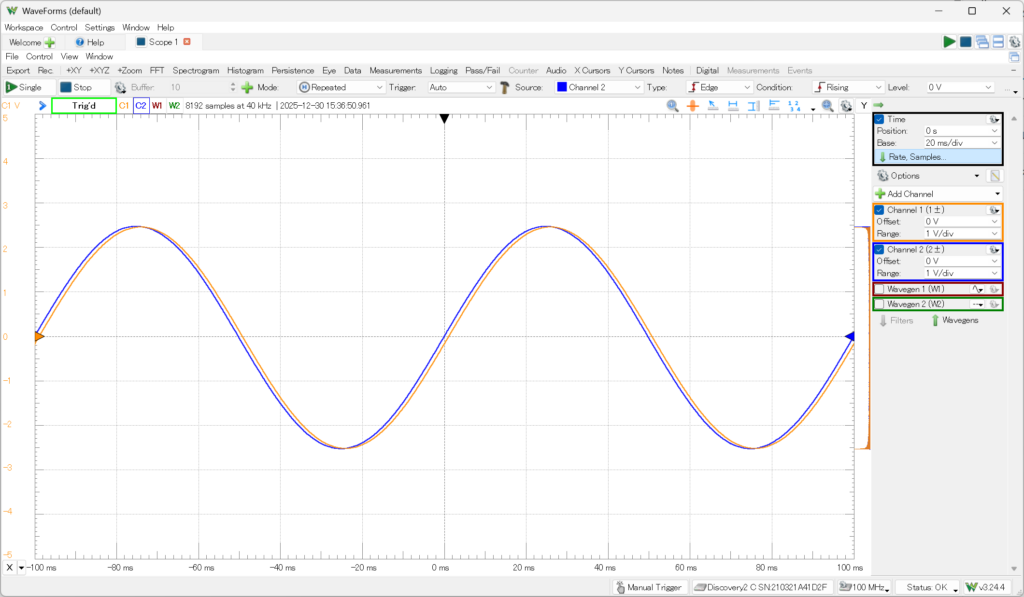
これはwave1を

とした時の入出力波形である。周期100msがτ=RC=1msに比べてかなり大きいので、振幅の減少や位相ずれも少ないが、周期を短くしていくと、

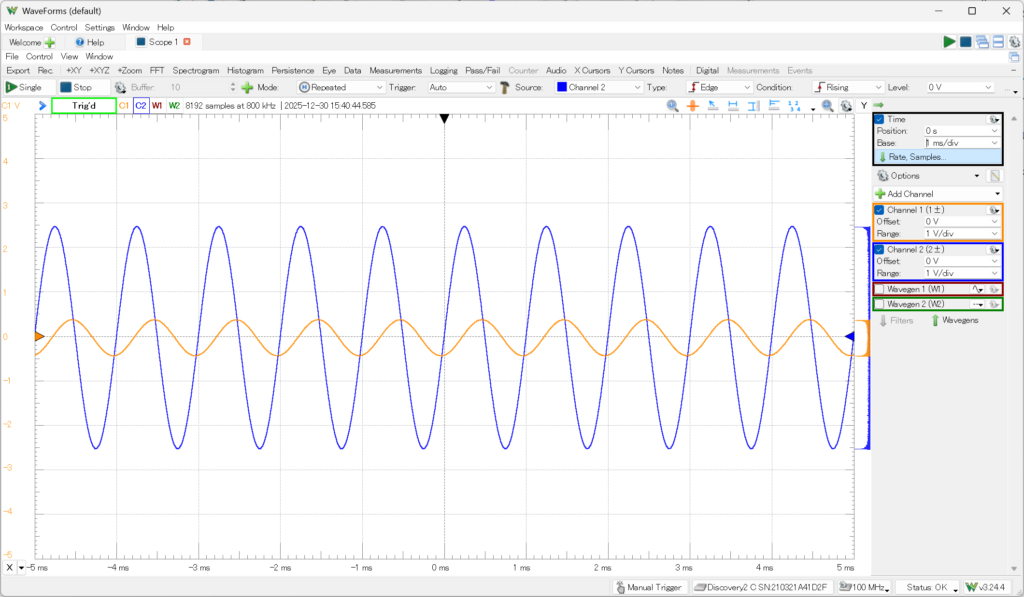
のように、振幅はかなり減少し、位相差も大きくなってくる。周波数に対して振幅比や位相差がどう変化していくかを示したものが、いわゆるボード線図と呼ばれ、マメに周波数を変えながら、振幅比や位相差を測定して周波数（対数目盛）に対してプロットしていけば得られる。この周波数応答はよく使われる計測対象なので、自動化可能で、WaveFormsの“Network”機能で可能だ。

ここでNetworkを選択、

等として、”Run”,途中では

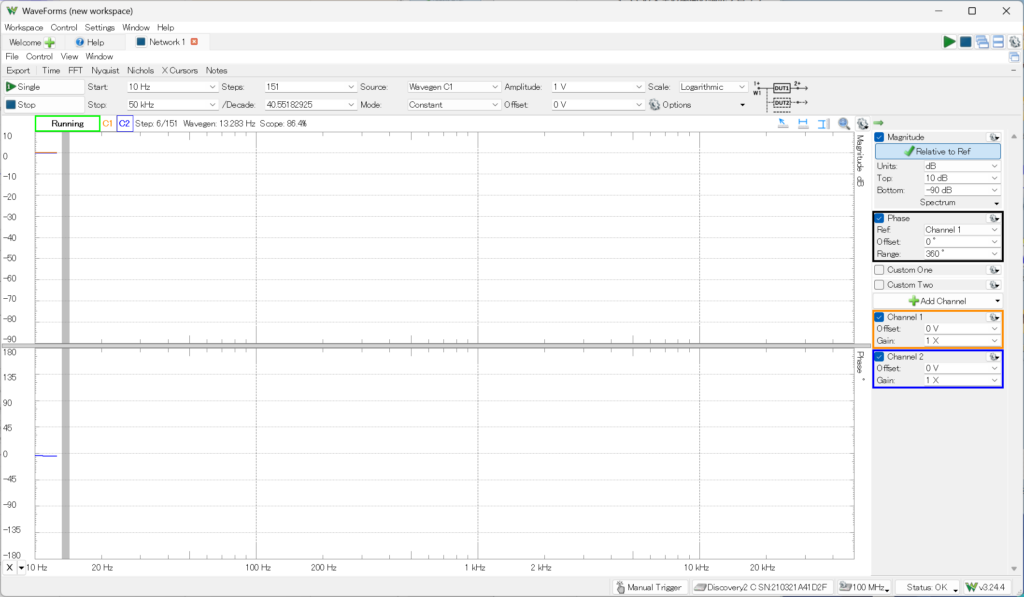
最終結果は、

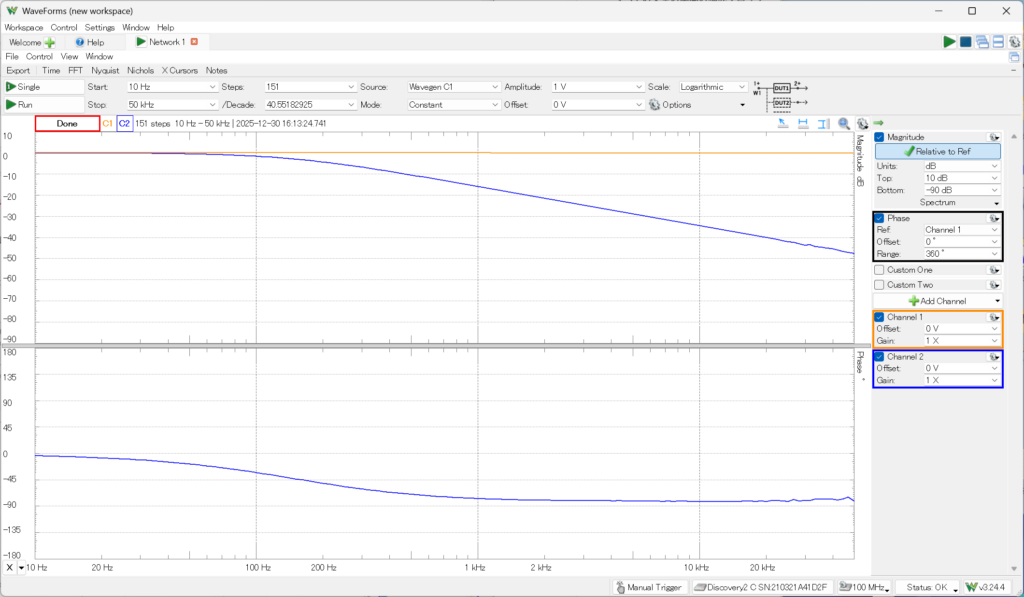
darkにすると、

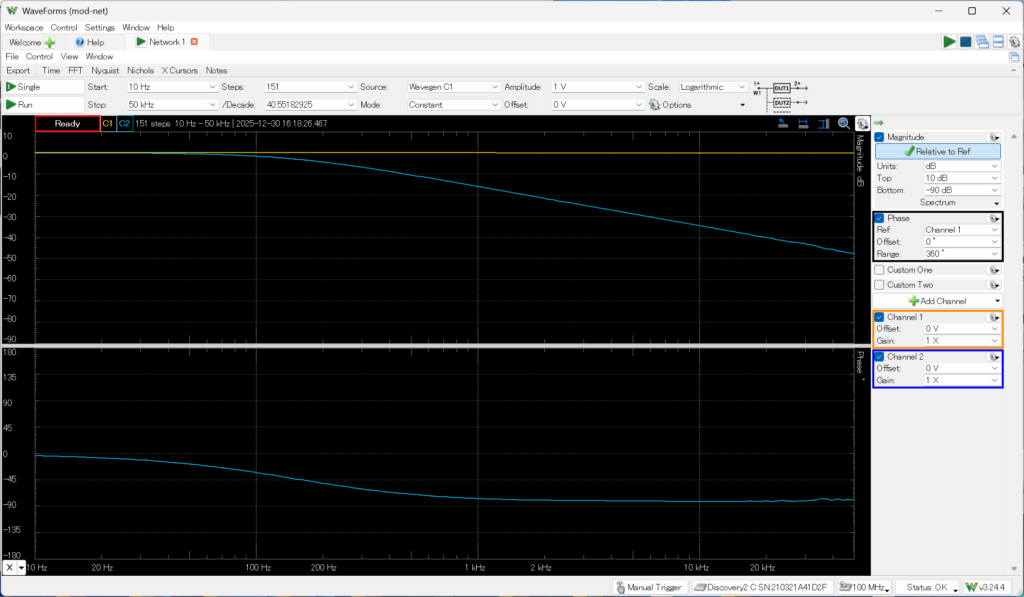
それらしい結果が得られた。周波数（対数目盛）に対して、ゲイン（振幅比）が1より下がって-3dB(0.707倍）になるところがカットオフ周波数である。RCの値とこの周波数fcの関係は、

である。時定数RCの次元は時間[t]なので、上式の左辺 $f_c$の次元は$[t^{-1}]$で単位時間内の周波数でHzであり、辻褄があっている。さてCR=1uFx1KΩなので、周波数を具体的に計算すると、

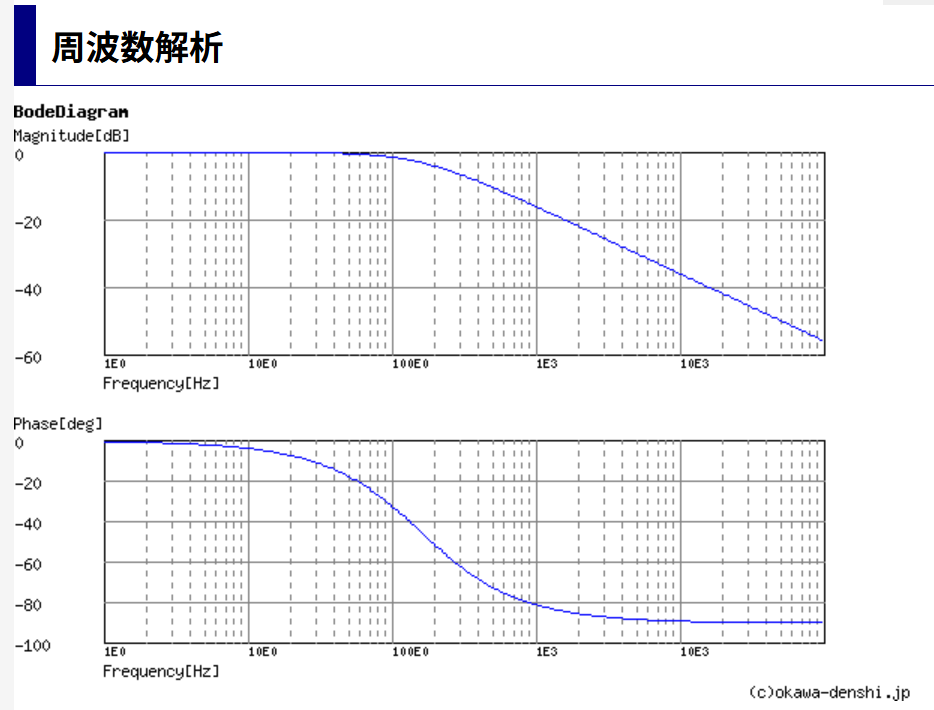
計算は、

ここで行いました。おまけでボード線図も出てます。

RCの配置をちょいと”曲げる”と、

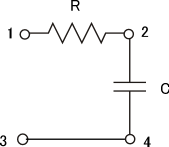
このようになり、1－3間に入力を入れ、2－4間から出力を取り出すような4つの端子を持ったフィルターと呼ぶ、ここでCとRを入れ替えると、

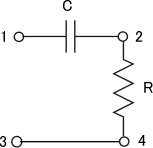
こうなるが、これも4端子フィルターになるが、ローパスではなくハイパスフィルターとなる。

2026/01/08(木) 9:08 AMにカットオフ周波数を具体的に計算する部分を追加しました。