テイラー展開とその応用

＃2　sin x および cos xの巾級数展開と一次近似

前記事から引用すると、テイラー展開ないしマクローリン展開は、

\(f(x) = f(0) + f'(0)\,x + \frac{f^{”}(0)}{2!}\,x^2 + \cdots + \frac{f^{({n})}(0)}{n!} \,x^n+ \cdots\)

と書けた。今f(x)がsin(x)ないしcos(x)とすると、それぞれの巾級数展開は、

\(\sin x=x-\dfrac{x^{3}}{6}+\dfrac{x^{5}}{120}+\cdots\)

\(\cos x=1-\dfrac{x^{2}}{2}+\dfrac{x^{4}}{24}+\cdots\)

と書ける。この多項式から、sin(x)は奇数次の項しか含まれないので奇関数であり、cos(x)は偶数次の項だけなので、偶関数ということがわかる。さらに今工学でよく使われる一次近似を当てはめる。つまり\(x\)が微少量の時、\(x^2\)以上の項をゼロと見なす近似である。とすると近似的に、

\(\sin x \approx x\)

\(\cos x \approx 1\)

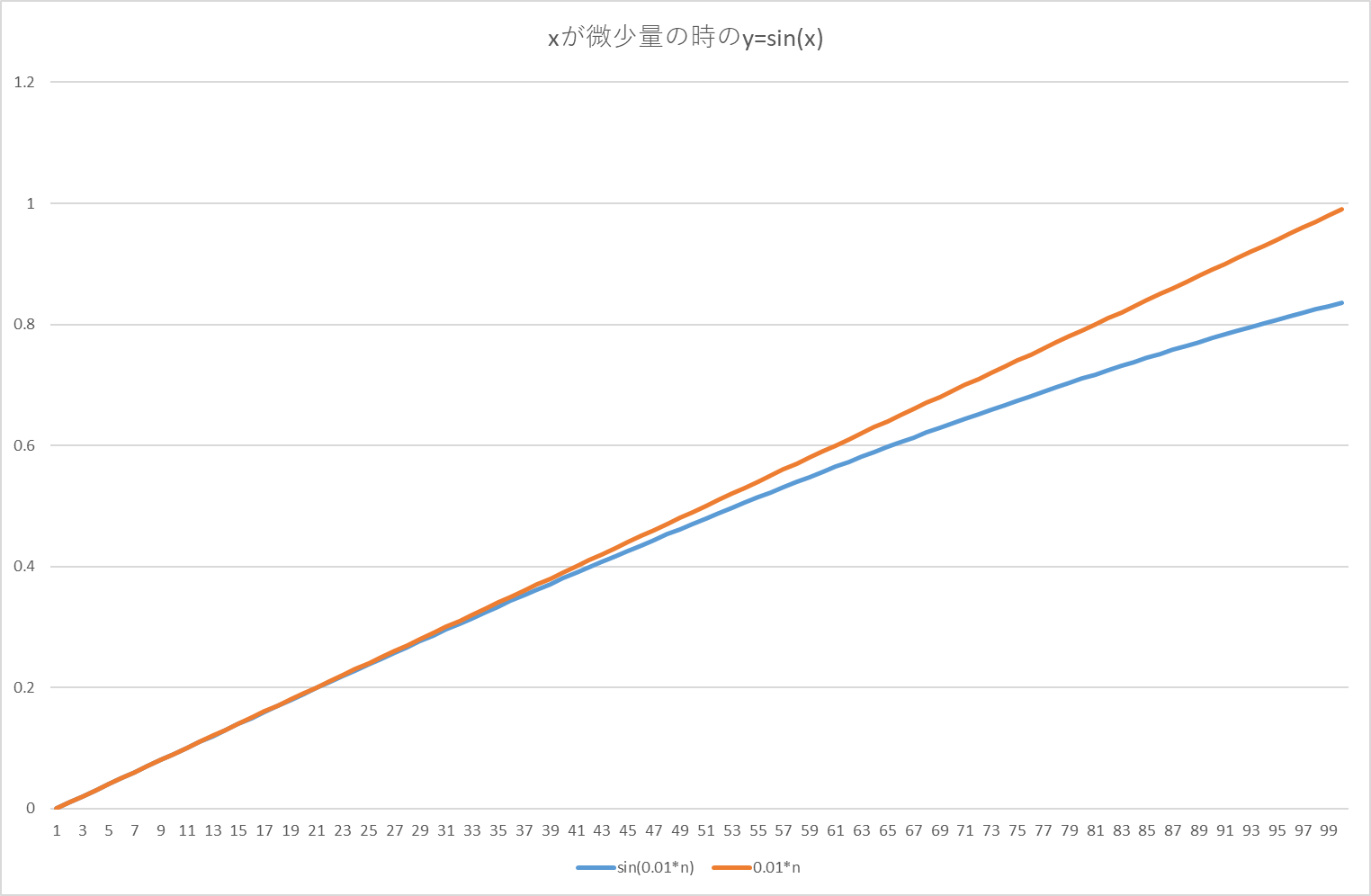
グラフで検分してみよう。Excelを使って、y=sin(x)のグラフについてｘ＝0付近を拡大すると、

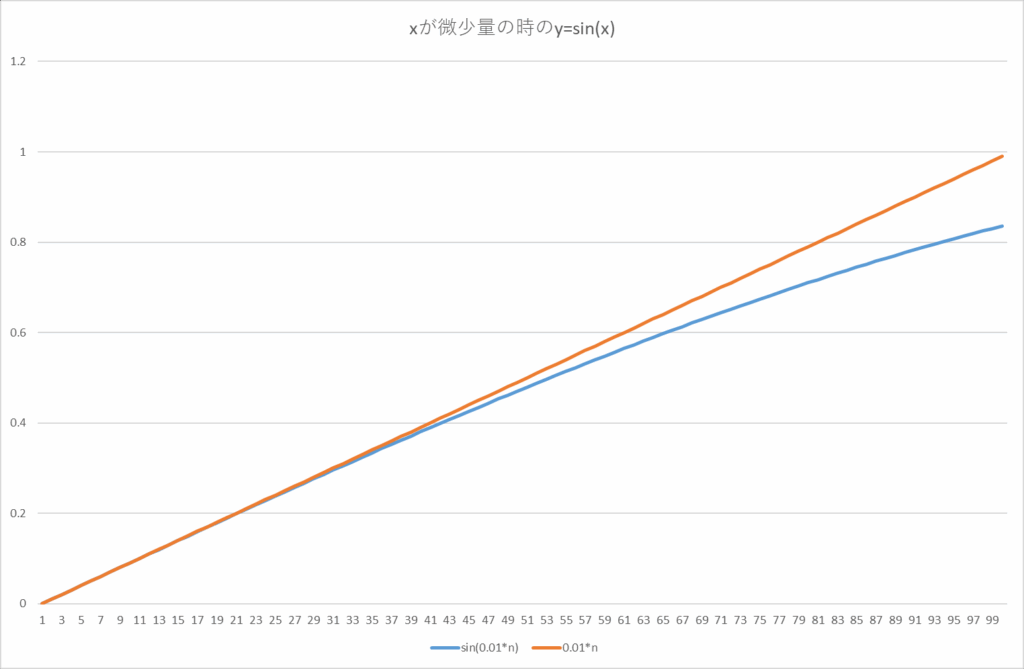
となって、xが小さい値の時はy=sin(x)とy=xの差が少なく、y=xで近似できそうだということがわかる。同様にy=cos(x)については、

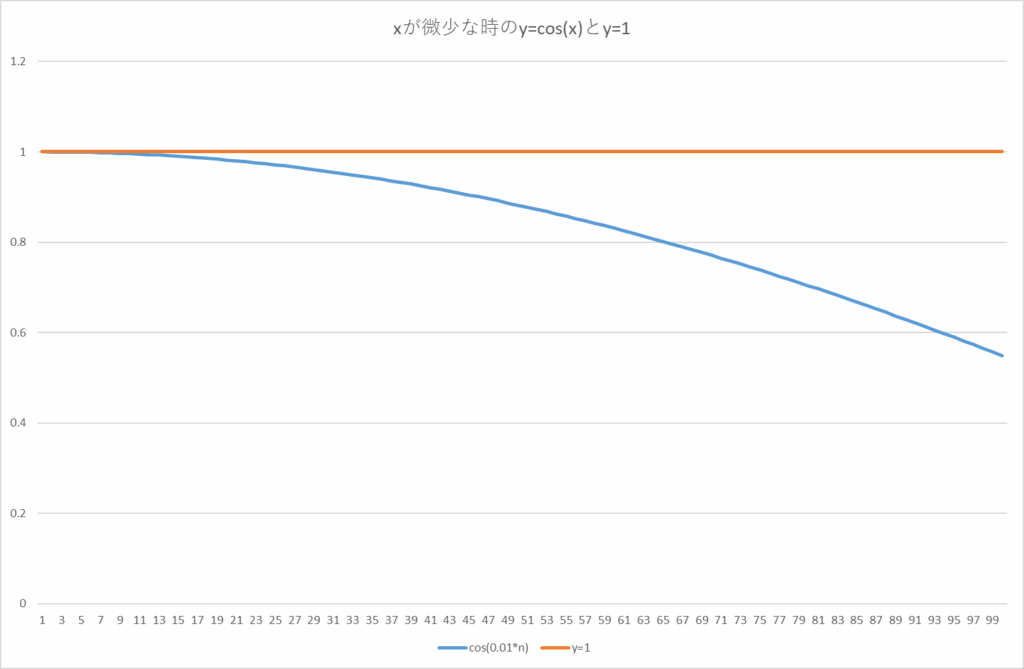
となりy=1と扱えることがわかる。公式によれば、

\(\sin^2{x} + \cos^2{x} = 1 \)

が成立してないといけないわけだが、xが微少な場合には、

\(\sin^2{x} + \cos^2{x} \approx {x}^2 + 1^2 = 1 \)

で辻褄が合っている。