テイラー展開とその応用

＃1　自然対数の底eの近似値を求めてみる

テイラー展開は、

\begin{eqnarray}
f(a + x) &=& f(a) + f'(a)\, x + \frac{f^{”}(a)}{2!}\, x^2 + \cdots +
\frac{f^{({n})}(a)}{n!}\, x^n + \cdots\
&=& f(a) + \sum_{k=1} \frac{f^{(k)}(a)}{k!}\, x^k
\end{eqnarray}

\(a=0\)の時をマクローリン展開といい、

\(f(x) = f(0) + f'(0)\,x + \frac{f^{”}(0)}{2!}\,x^2 + \cdots + \frac{f^{({n})}(0)}{n!} \,x^n+ \cdots\)

今具体例として、\(f(x) = e^x\)の場合を考える、\(e^x\)をｘについて微分すると、何回微分しても\(e^x\)となり、しかも\(e^0 = 1\)なので、

\(e^{x}=1+x+\frac{x^{2}}{2!}+…+\frac{x^{n}}{n!}+… \)

\(x = 1 \)を代入すると、

\(e = 1 + 1+\frac{1}{2!}+…+\frac{1}{n!}+… \)

n項はnの増加で急速に減少するので、その状況をExcelを使って数値計算してみよう。

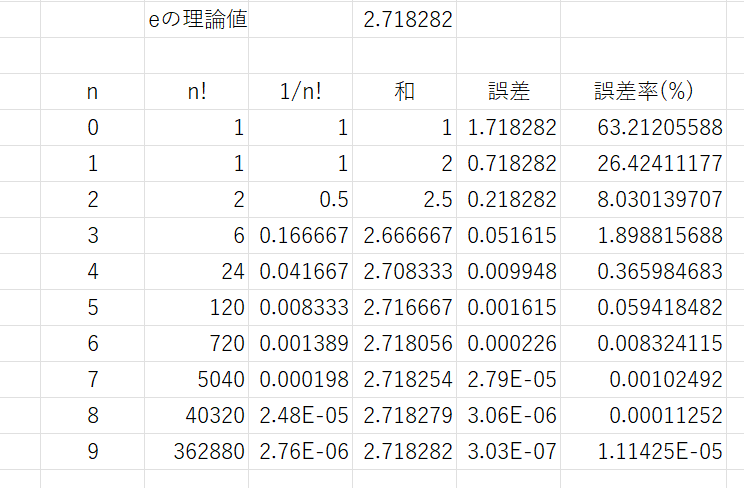
上の表で明らかなように、n=5くらいまでの計算で誤差率0.05%になるので、工学的には十分な精度と言える。グラフは、

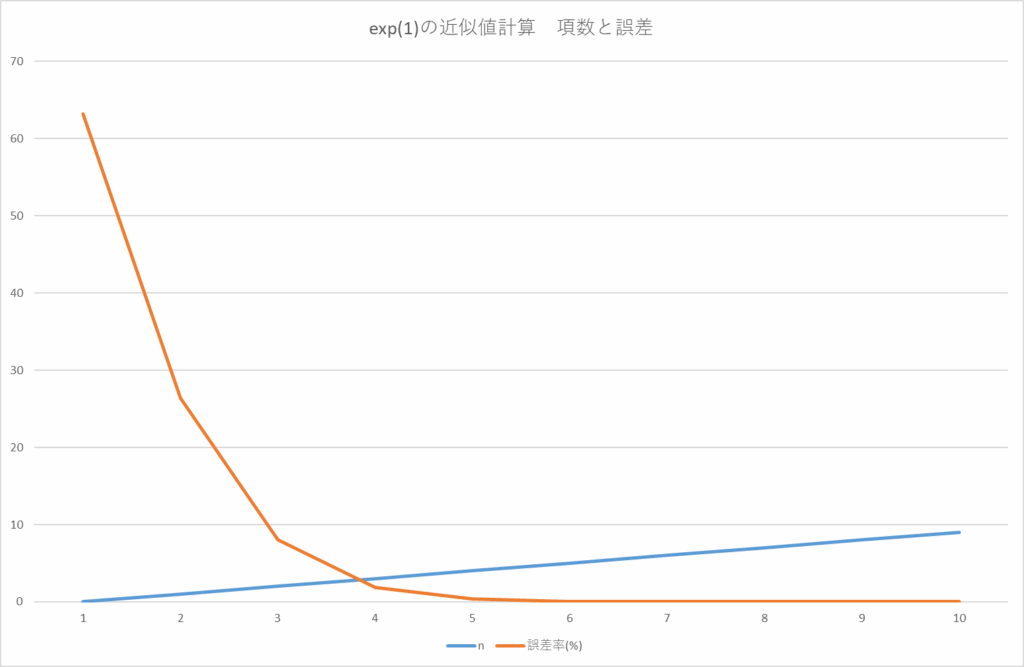
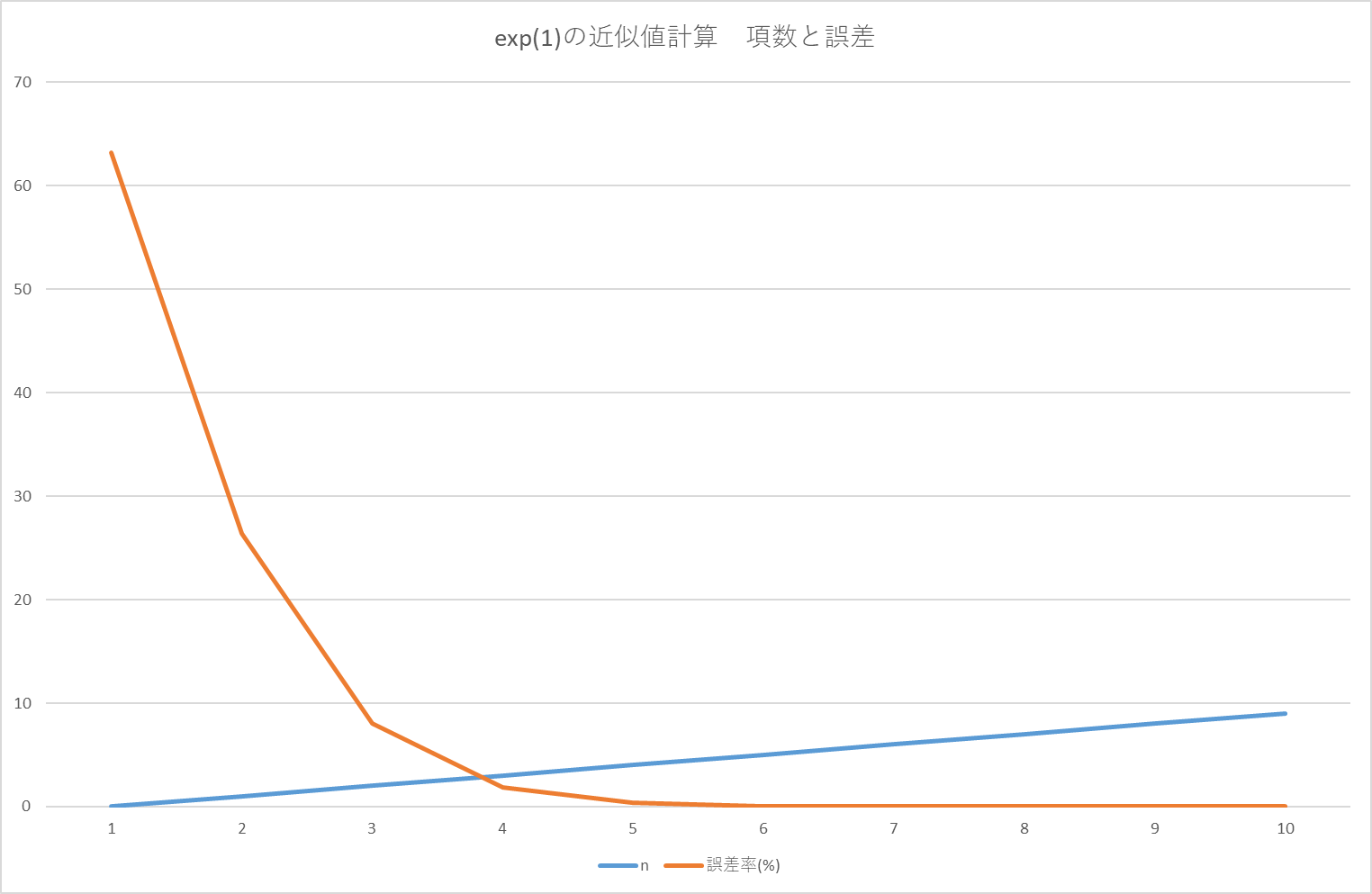
nの増加につれて、急速に誤差が減少していくことがわかる。全てのf(x)に対してこううまく行くわけではないが、基本的にCPUは四則演算しかできないので、近似値を求めるときの使用公式の収束性は重要である。