R.M.S.値とは何か?
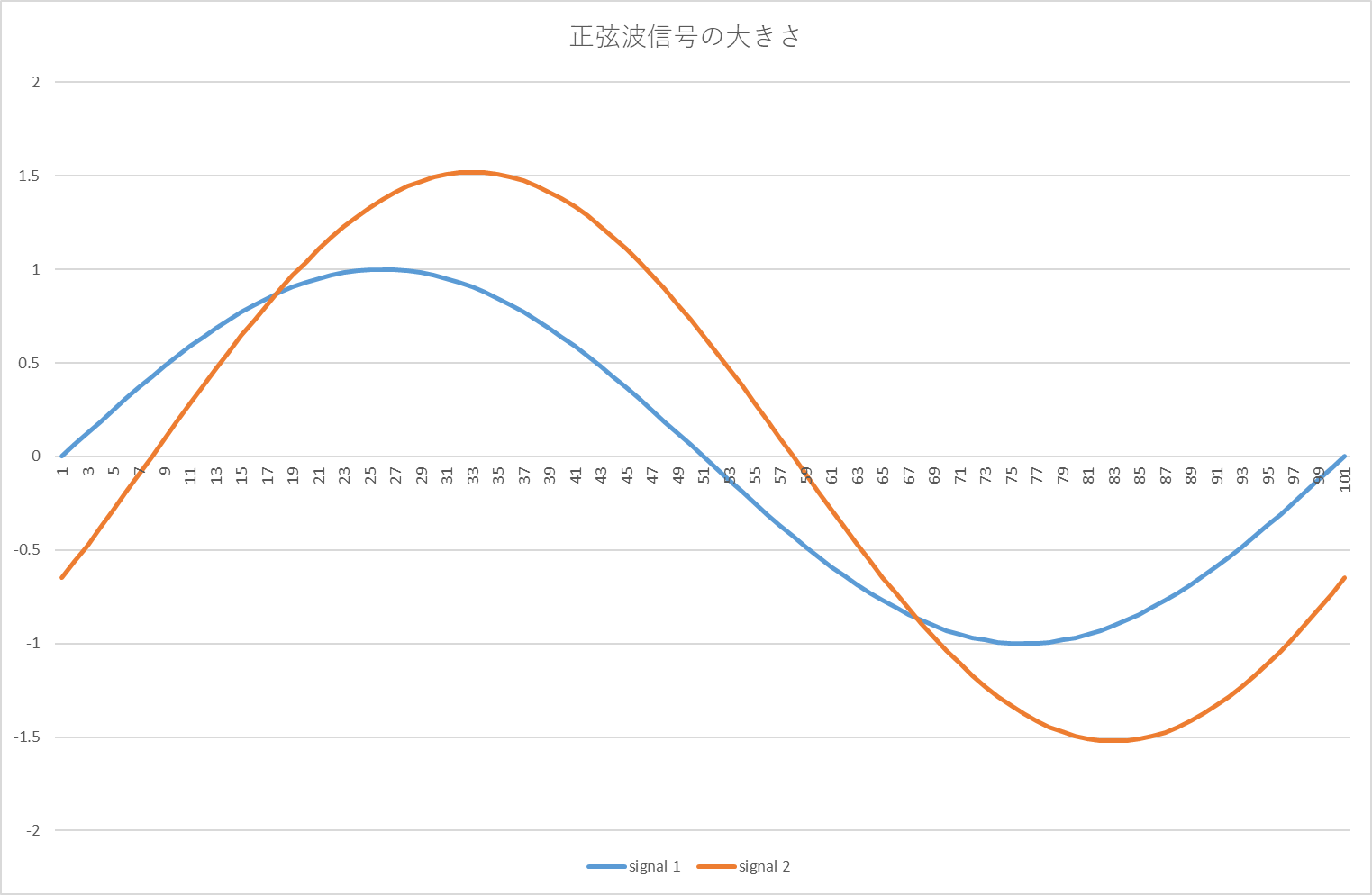
例えば、二つの信号を計測した結果が下図のようであったとする。
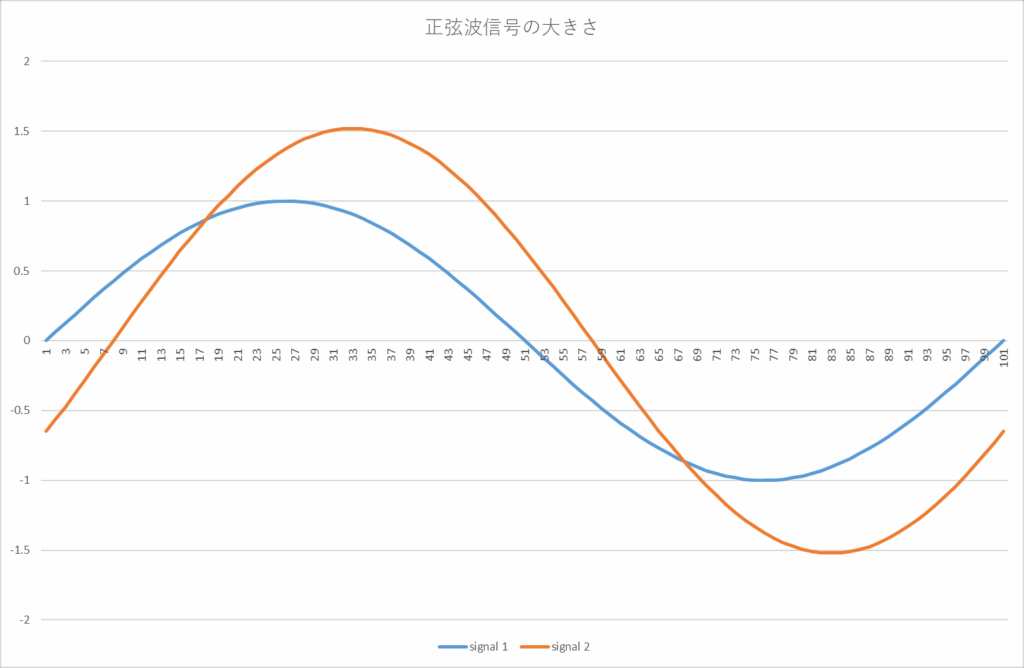
二つの信号signal 1(青色)とsignal 2(橙色)とではどちらの信号が大きいだろうか?見ればわかるようにsignal 2の方が定性的には”大きい”と言えるが、定量的には”何倍大きい”と言えるだろうか?両方の信号の時間平均はともにゼロである。(プラスマイナス交番信号である。)全振幅はかろうじてsignal 1が2,signal 2が3位とグラフから見てとれるが、正確な値とは限らない。このような交番信号ないし波形の大きさの評価をする場合には、R.M.S.値を使う。定積分の演習問題としては適当なレベルであるので、ここで練習がてら具体的に計算してみよう。まず
R.M.S.とは Root Mean Squareの省略語である。Rootは平方根を取る、Meanは平均を取る、Squareは自乗するということなのだが、逆順にアプライする。つまり、自乗して、時間平均を取り、最後にルートを取るという手順だ。
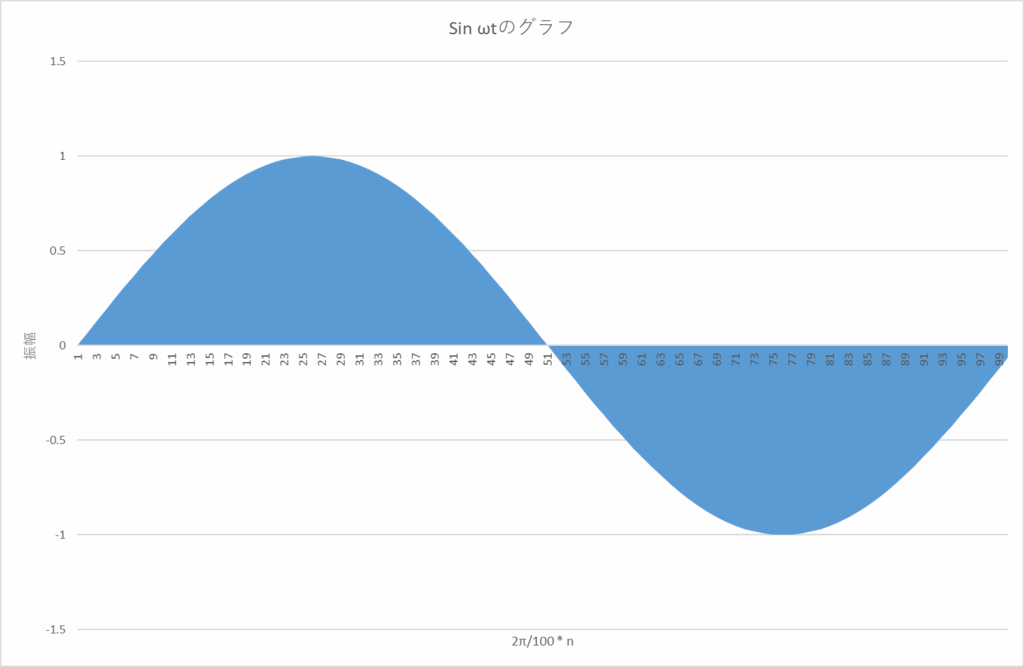
自乗(2乗)すると、
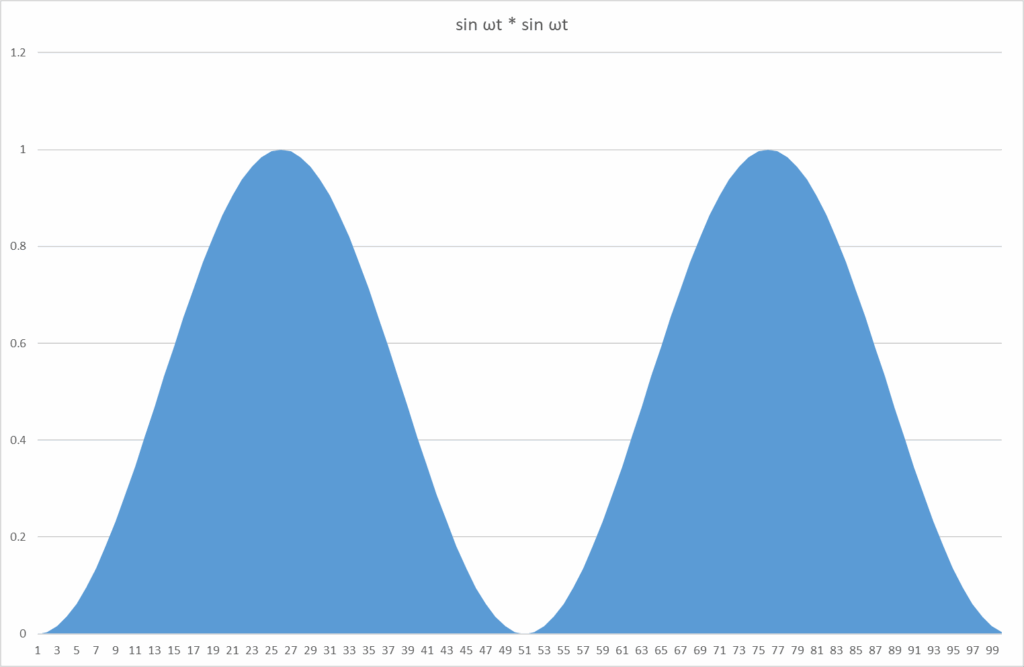
輪郭は正弦波じゃないの?って、良い勘してますね。倍角の公式というのがあって、それを\(\sin ^2{x}\)について解くと、
\(\displaystyle \sin ^2 {x} = \frac{1- \cos{2x}}{2}\)
となるので、辻褄はあう。sinの自乗は、cosの倍角(ピッチ2倍)で上にシフトしてものの1/2である。さて上図の青い部分の面積を求めたい、区間\(0~\dfrac{\pi}{2}\)は全体の1/4なので、面積全体を4Sとすると、
\(\displaystyle S = \dfrac{1}{2}\int _{0}^{\dfrac{\pi }{2}}\left( 1-\cos 2x\right) dx\)
\( = \dfrac{1}{2}\left[ x-\dfrac{1}{2}\sin 2x\right] _{0}^{\dfrac{\pi }{2}}\)
\( = \dfrac{\pi}{4}\)
よって区間全体の積分値は、\(\pi\)となる。区間の幅は2\(\pi\)なので、平均の高さ(時間平均)は、1/2となり、これの平方根は
\(\dfrac{1}{\sqrt 2}\)有理化するために、分母分子に\(\sqrt 2\)をかけると、\(\dfrac{\sqrt 2}{2}\)
なので振幅(片振幅)1の正弦波のR.M.S.値は約0.707ということになる。身近での典型的な正弦波信号の例は、家庭用交流AC100Vであるけれど、これはR.M.S.値が100ということなので、最大振幅は逆数をかけて約141Vということになる。平均的には100Vと見なせるという意味で実効値とも言われる。以上は正弦波の場合であったが、三角波の場合も計算できる。正弦波と三角波の関係は、
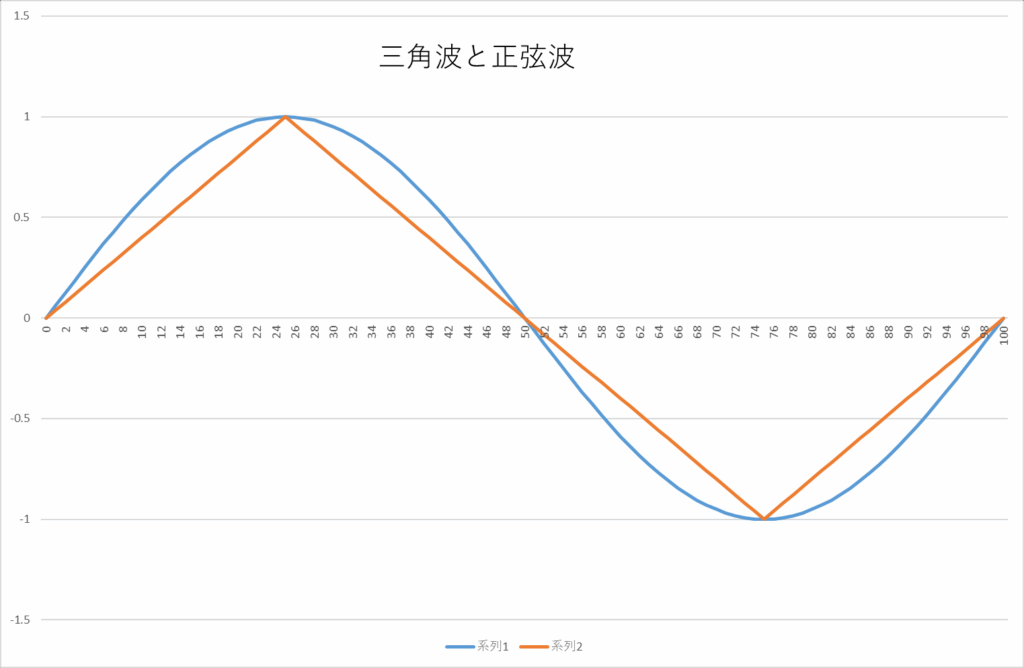
常に正弦波の強度>三角波の強度なので、当然ながら実効値も三角波の実効値が小さい。波形が式で与えられていれば、正弦波の時のようにR.M.S.を解析的に定積分を用いて求めることができる。トライしてみてください。実際の信号の場合、得られるものがきれいな正弦波ないし三角波ということはまずない。そういう場合にも信号の強度を計算する必要があれば、AD変換したデジタルデータを元に数値積分というか和を求めて平均することになる。実際は、一定周期でサンプリングしたデータを元にR.M.S.値を求める。アナログ的にこれをやるのは困難だが、近代的な計測器はデータアクイジションの技術で可能としている。検索すればいくらでも例示はできるが、
等である。


コメント