数学的工学的に有用な公式
まずテイラー展開とは、関数\(f(x)\)の任意の値\(a\)からのオフセットで\(f(x)\)を表現する公式で、
\({\displaystyle f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^{n}}\)
と書ける。ここで\(f^(n)\)はn階のfの導関数である。\(a=0\)の時の形式を特にマクローリン展開と呼び。総和でなく級数で書くと、
\(f(x)=f(0)+f'(0)x+\dfrac{f”(0)}{2}x^{2}+\dfrac{f^{(3)}(0)}{6}x^{3}+\cdots\)
となる。この公式を使って、\(f(x)=e^x\)の場合を具体的に計算してみよう。
\(e^x\)の導関数（微分）は\(e^x\)であるから。何回というか何階微分しても同じ。\(e^0\)は1なので、\(e^x\)のマクローリン展開を書くと、
\(e^x = 1 + x + \dfrac{1}{2!}x^2 + \dfrac{1}{3!}x^3 + \cdots\)
となる。\(x=1\)として右辺を計算してみよう。1/n!という項は、nが大きくなるにつれてn!が急峻に増大するので、微少な値になる。何次の項まで計算すれば良好なeの値が得られるだろうか？WindowsのアプリケーションであるExcelを使って見よう。第ｎ項に対して、n,1/n!,その項までの和、誤差、誤差率（％）を、縦軸にｎ横軸に各項目を並べたスプレッドシートは、以下のようになる。
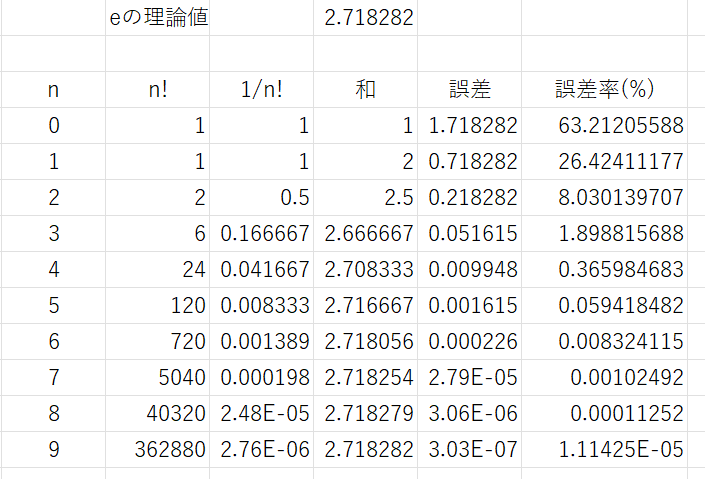
スプレッドシート自体は、https://ghost.mydns.jp/wordpress/wp-content/uploads/2024/11/exp-x-approx.xlsxからダウンロードできます。グラフを描くと、
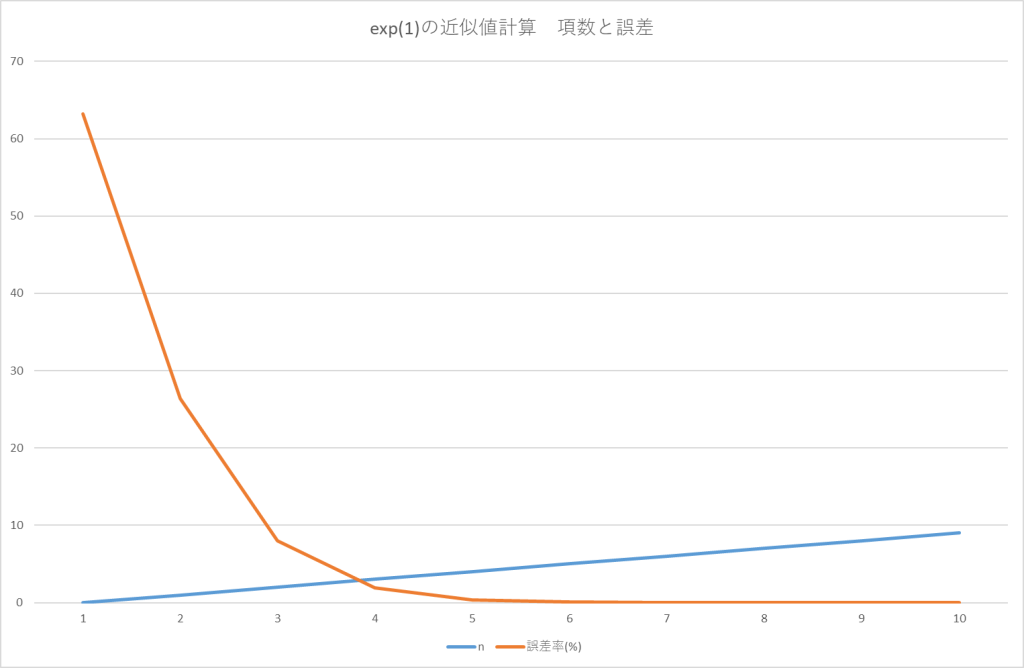
のようになる。
誤差率は急速に減少して、およそ第6項くらいで計算を打ち切っても誤差率0.008％程度である。近似値としては充分だろう。特に工学分野では有効数字3桁（昔のアナログ時代の話）程度で充分なので、これで良しとできる。
コメント