定積分の初級練習問題ですね。前記事から続く。
三角波をまず作ります。区間は0~2πで100分割として、グラフを描くと、
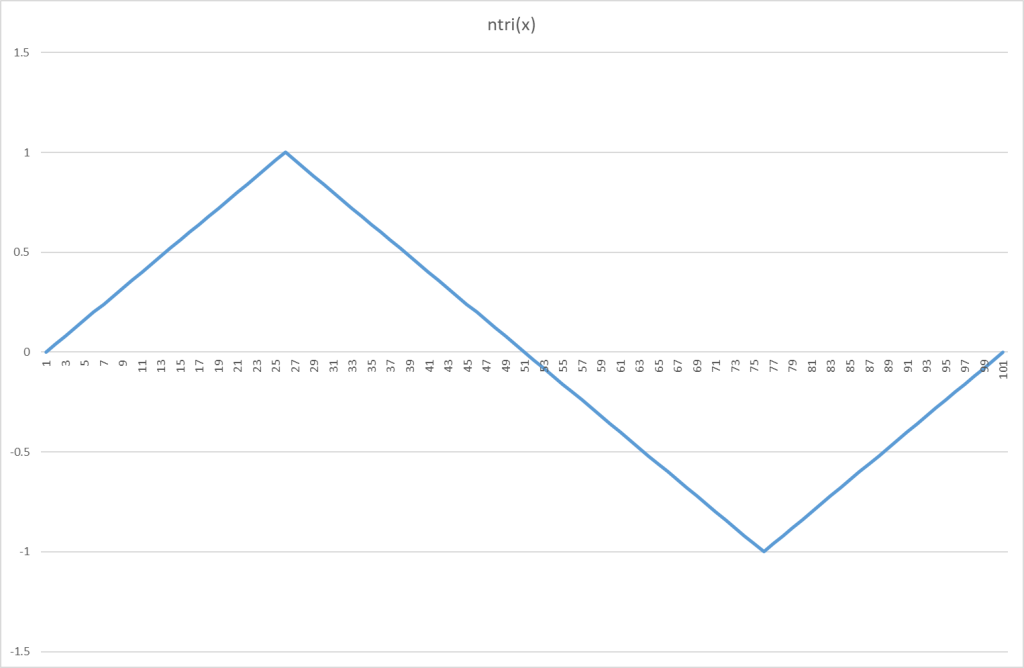
まず自乗します。Squareですね。さらに計算すべき面積を明示するために領域を色で塗ると、
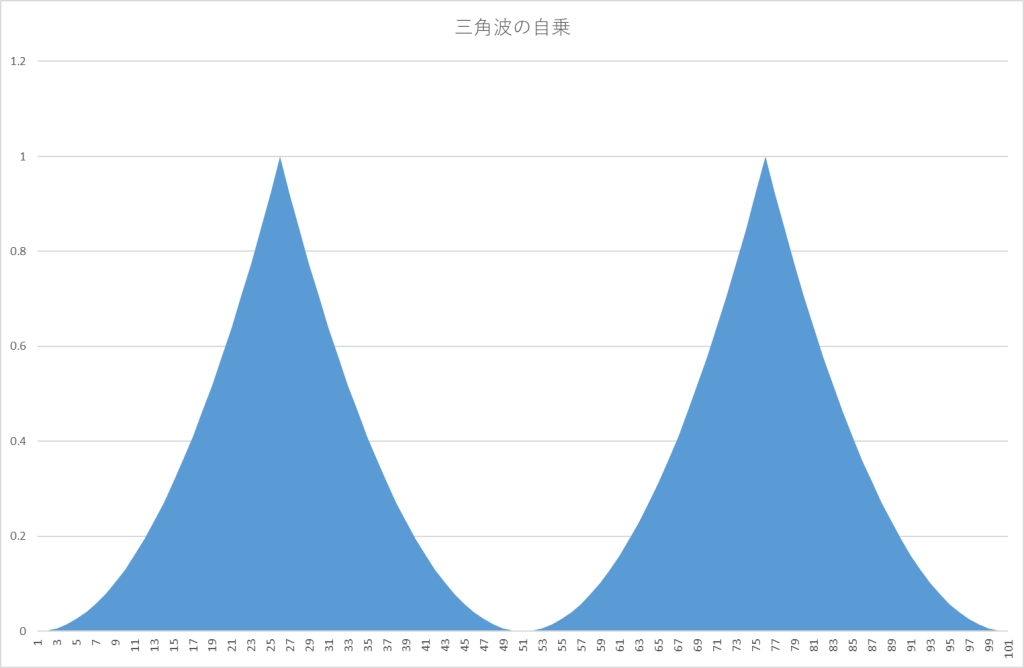
上図の1/4区間の面積を解析的に求めます。つまり全体の面積をSとすると、S/4(上図でx軸が0~24の範囲)を求めます。この区間で、x=0でy=0,x=π/2の時y=1なので、横軸と縦軸の関係は \(y=(\dfrac{2}{\pi})^2x^2\) となりますから、
\(\displaystyle\dfrac{S}{4}=(\dfrac{2}{\pi})^2\int_0^\dfrac{\pi}{2}x^2dx\)
\(=(\dfrac{2}{\pi})^2 \left[\dfrac{1}{3}x^3\right]^\dfrac{\pi}{2}_0\)
\(=\dfrac{4}{\pi^2}\dfrac{1}{3}\dfrac{\pi^3}{8}\)
\(=\dfrac{\pi}{6}\)
したがって\(S=\dfrac{2}{3}\pi\)です。
区間の幅は、0~\(2\pi\)なので、平均高さ、つまり矩形にならしたとするとその値は、面積を幅で割ればいいので\(\dfrac{1}{3}\)、最初に自乗してますから次元を合わせるためにこの値の平方根を取って、\(\dfrac{1}{\sqrt3}\)が答えとなります。これがR.M.S値ということになります。有理化すると、その値は\(\dfrac{\sqrt3}{3}\)となり約0.577。前記事の最後の予想通り、正弦波の場合より実効値が小さいことがわかりました。



コメント