デジタル論理回路での正論理と負論理

フリップーフロップでの例　RC初期化回路の応用

以下のようなNANDゲートを2個たすき掛けにしてフリップ-フロップを構成した時の入力と出力の関係を表す真理値表がすぐに頭に浮かぶだろうか？

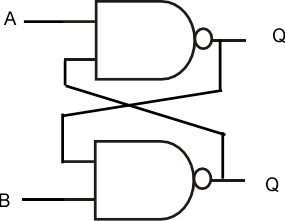
これは入力側を正論理で書いてしまったために、回路の”意図”がすぐに分からない表現になってしまっている。一個のNANDゲートについては、以下のような入出力の関係にあることはよく知られている。具体的な素子としては7400で一番最初の型番だからこれが取り上げられることが多い。

NANDのシンボルと真理値表

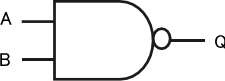
入力A	入力B	出力Q
L	L	H
H	L	H
L	H	H
H	H	L

言葉で表現するとNANDは入力の両方(AND)がactive(H)になった時だけ出力がactive(L)になる。

しかしこれは正論理でのシンボルであり、負論理（入力がLの時に意味がある、activeである、信号が出る）の場合には、以下のように表現した方が分かりやすい。つまりInverted ORである。

I-ORのシンボルと真理値表

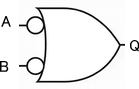
入力A	入力B	出力Q
L	L	H
H	L	H
L	H	H
H	H	L

言葉で表現すると、入力のどちらか(OR)がactive(L)となったら出力がactive(H)になる。真理値表を見ればわかるようにこれら二つは、シンボルだけが異なるが、全く同じ機能である。入力側と出力側の論理が逆になっているだけである。で、最初に戻ってフリップーフロップをI-ORのたすき掛けで書くと、

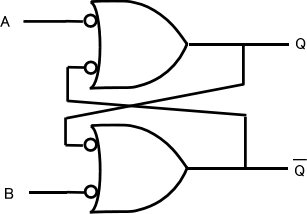
このようになるが、ここで入力AとBの組み合わせと出力Qおよび\(\bar{Q}\)の関係は、

入力A	入力B	出力Q	出力Qバ
L	H	H	L
H	L	L	H
H	H	不変	不変
L	L	禁止	禁止

テーブル内に\(\bar{Q}\)がうまく書けないので、”Qバ”となってます。言葉で表現すると、入力AあるいはBのラインがactive（L）になると、対応した出力側がactive(H)になるというのが記号を見るだけで分かるわけです。という理由で、こう書くべきだということです。これをMIL記法といいます。さて、ここでようやく前の記事のRC遅延回路微分方程式を解くが出てきます。それを組み込むと、

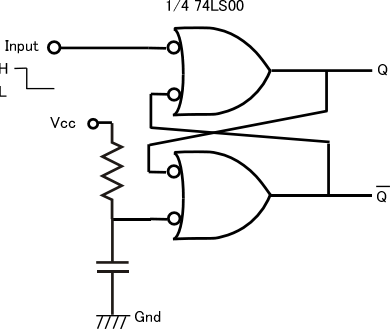
こんな回路になりますが、電源がオンになり回路が充分安定した時点で下側の入力はL->Hとなりますので、Qの初期値はLになります。その状態で上側の入力にH->Lの信号が来た時点でQはHとなり以降そのままの状態が維持されます。上側の入力端子はノイズ対策を考えて、プルアップ抵抗経由でVccにつなぐのが吉ですが、上図ではごちゃごちゃするので省略してます。上側にスイッチ入力をつけると、そのスイッチのチャッタリングを防ぐことができます。NANDって大概2個くらいは余っていますから、この回路を組むことは多いです。今は、なんらかのプロセッサがあり、ソフトウエアないしファームウエアで初期化などはしますから、こうしたワイヤードロジックはあまり目にしなくなりました。