もっとも基礎的な式の変形を学ぶ ”何々について解く”をオームの法則に適用する
\(V=IR\)
この公式はオームの法則といって、以下の回路図において、電源電圧(V ボルト)、抵抗器Rの抵抗値(Ω オーム)、回路に流れる電流Iの値(A アンペア)の関係をあらわしたものである。
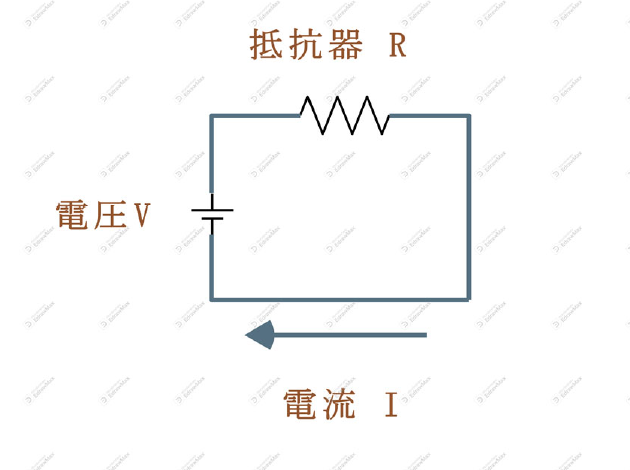
三つのパラメーターの関係であるが、既知の二つのパラメーターから残りのパラメーターを求める式ともいえる。つまり
\(V=IR\)
は、電流値Iと抵抗値Rがわかっている時に、電圧の値を求める式である。
同様にI=,R=の式を求めておこう。(一番簡単な式の変形である。)上の式をIについて解くと、つまり左辺がI=である形式にするには、左辺と右辺を入れ替えて、
\(IR=V\)
ここで両辺をRで割ると、
\(I=\dfrac{V}{R}\)
となるので、Iについて解けた。(解けたというほどではない。)
Rについて解くには、同式の両辺をIで割って、
\(R=\dfrac{V}{I}\)
I=の式で、左辺のIと右辺分母のRを入れ替えても良い。常に成り立つ。
何を求めるかに応じて、この三つの式を使い分けるのが誤らないコツである。ただし憶えるのはV=IRだけで良いと思う。



コメント