復習してみようか
まず\(\sin x\)のマクローリン展開は、
\(\sin x=x-\dfrac{x^{3}}{6}+\dfrac{x^{5}}{120}+\cdots (1)\)
これは奇関数である。つまり\(f(x) = -f(-x)\)が全ての\(x\)で成立する。(1)式の右辺には奇数乗の項しかないので、自明。これはグラフ的には何を意味するだろうか?\(\sin x\)を表す曲線は、原点について対称、つまり原点周りで点対称であるということだ。以下にグラフを示す。通常はExcelを使っていたが、座標軸が綺麗に書けるので、今回はdesmos.comを使った。urlはhttps://www.desmos.com/calculator/w9jrdpvsmk?lang=ja
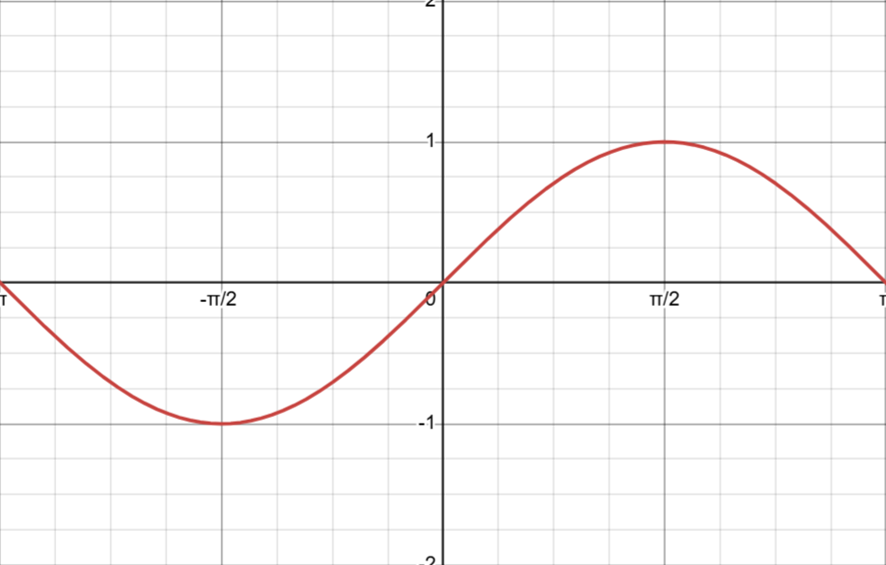
他方\(\cos x\)のマクローリン展開は、
\(\cos x=1-\dfrac{x^{2}}{2}+\dfrac{x^{4}}{24}+\cdots (2)\)
この式の右辺は、今度は偶数乗の項のみなので、偶関数。つまり\(f(x) = f(-x)\)が全ての\(x\)で成立する。従ってそのグラフは、y軸に関して線対称となる。
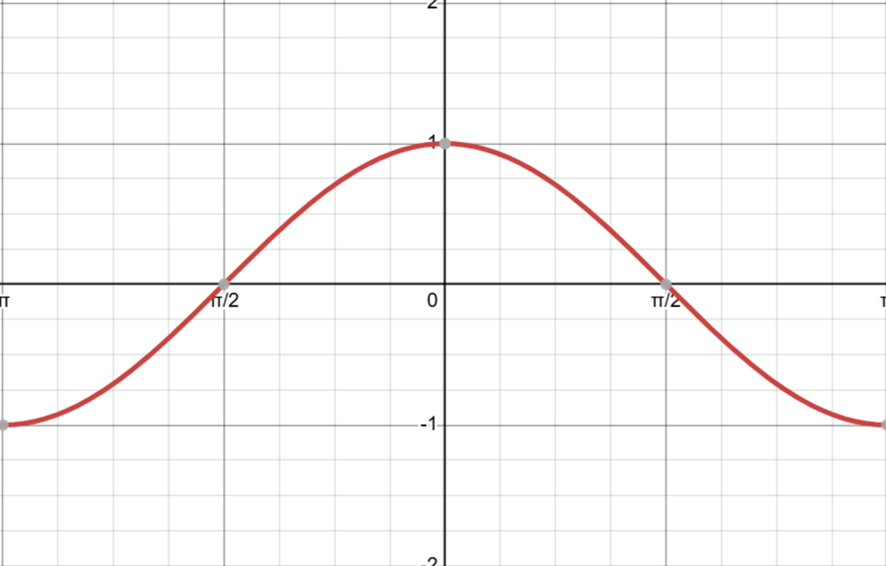
両方を同時に表示させることも可能。
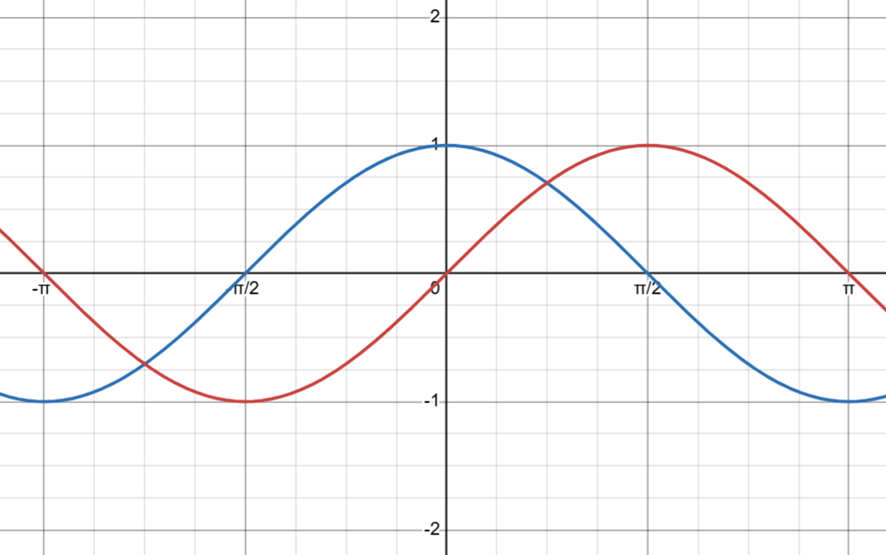
このサイトではもっと面白いデモもみることができる。例えば、
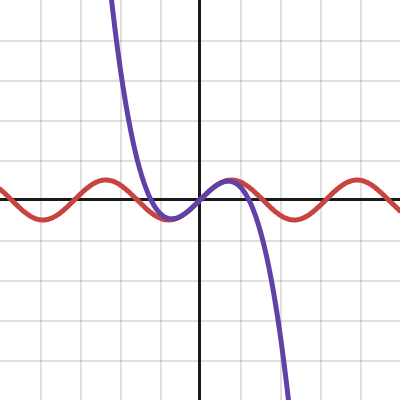
微積分:sin(x)のテイラー展開
Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equa...
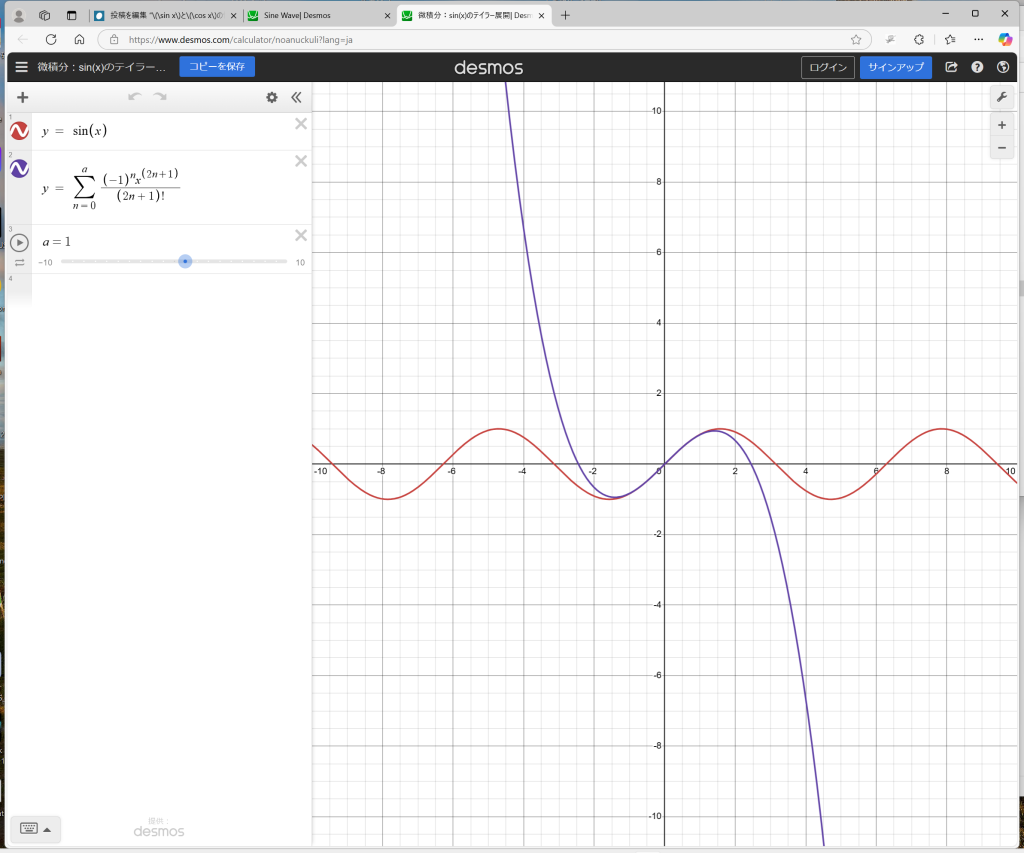
微積分:sin(x)のテイラー展開というものでは、a=1を右にドラッグすると高次の関数でsin(x)に漸近する様子をアニメーションで見ることができる。a=10とすると、
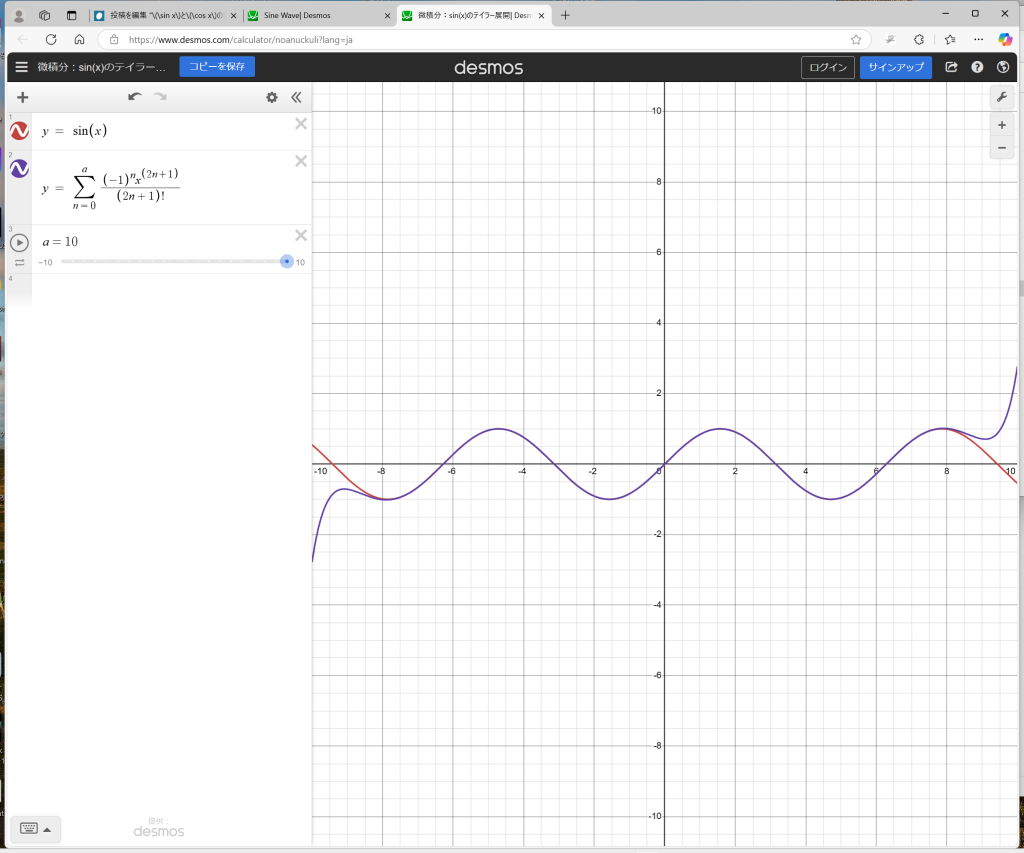
となって適合する範囲がかなり広くなる。高次までの級数の和が次第にsin(x)に近くなってくる様子がよくわかります。



コメント