運動方程式を解く＃1

一次元直線運動の場合

下図のような状況を考える。

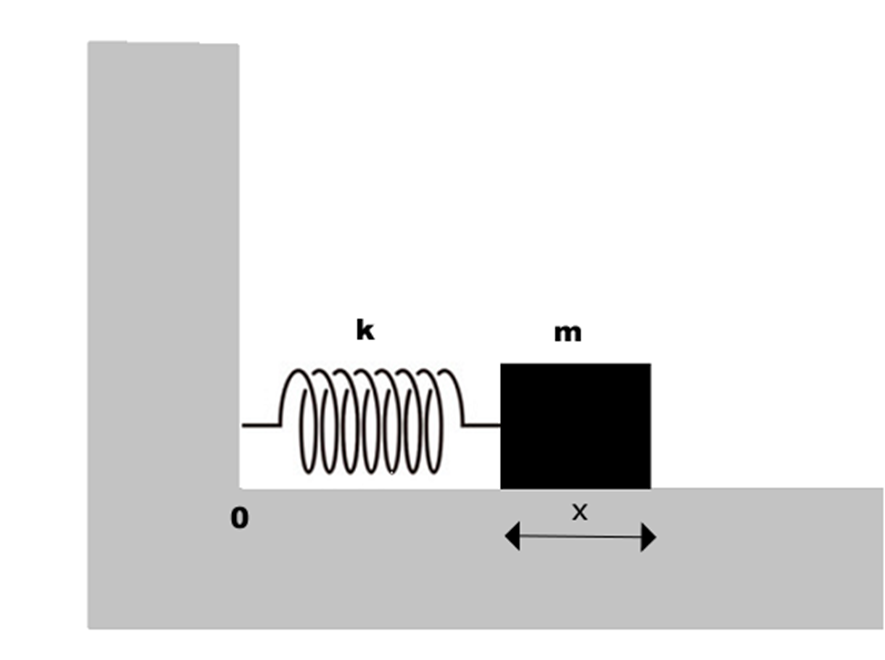
ばね定数ｋのバネと質量ｍの物体が連結されており、摩擦のない床の上で運動する場合を想定する。この系での運動方程式は、

\(F=kx=-ma\)

で、aは加速度つまり\(x\)の2階の時間微分\(\ddot{x}\)なので、結局

\(kx=-m\ddot{x}\)

となる。これは定数係数の2階同次線形微分方程式であり、\(\omega^2=\dfrac{k}{m}\)とすると一般解は、

\(x=A_1\cos \omega t+A_2\sin \omega t\)

となり、初期位相を\(\alpha\)とすると、

\(x=A\cos(\omega t + \alpha)\)

となり角速度\(\omega\)初期位相\(\alpha\)振幅Aの単振動である。あとは初期条件から定数を決めれば良い。

まず角速度\(\omega^2=\dfrac{k}{m}\)なので、この系の振動の周期Tは、\(2 \pi\)を\(\omega\)で割ったものになるので、

\[T=\dfrac{2 \pi}{\omega}=2 \pi \sqrt{\dfrac{m}{k}}\]

そして初期条件として\(t=0\)の時には\(x(0)=A\)とすると初期位相\(\alpha=0\)なので、最終的には、

\(x(t)=A\cos(\omega t)\)

となる。