RC直列回路での充電 時定数
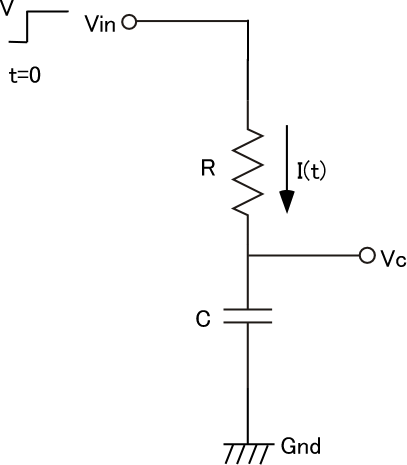
上図のように抵抗Rを通してコンデンサCに充電する状況を考える。時刻t=0で電圧はVとすると、コンデンサの電圧Vcはどのように変化するだろうか？時刻tの時に回路に流れる電流をi(t)とする。時刻tの時に、抵抗Rの両端の電圧は、オームの法則(V=IR)により、Ri(t)。コンデンサの両端の電圧VC=Vcは、コンデンサの式Q=CVc（ただしQはコンデンサに蓄積されている電荷、Cはコンデンサの静電容量）により、\(Vc=\dfrac{Q}{C}\)。従って、
\(V=Ri(t)+\dfrac{1}{C}\int i(t)dt\)
これはi(t)に関しての微分方程式なので、解法はいくつかあるけども、ここではラプラス変換を用いた解法を取り上げます。上の式の両辺のラプラス変換は、
\(V\cdot\dfrac{1}{s}=R\cdot I(s)+\dfrac{1}{C}(\dfrac{I(s)}{s}+\dfrac{q(0)}{s})\)
初期条件としてq(0)=0とすると、結局上の式は、
\(V\cdot\dfrac{1}{s}=R\cdot I(s)+\dfrac{1}{sC}\cdot I(s) \)
この式をI(s)について解くのであるが、
\((R+\dfrac{1}{sC})\cdot I(s) = \dfrac{V}{s}\)
両辺を\(R+\dfrac{1}{sC}\)で割ると、
\(I(s) = \dfrac{V}{s(R+\dfrac{1}{sC})}\)
\(= \dfrac{V}{R}\dfrac{1}{s+\dfrac{1}{RC}}\)
I(s)をラプラス逆変換してi(t)を得る、
\(i(t)={\mathcal L}^{-1}[I(s)]\)
\(={\mathcal L}^{-1}[\dfrac{V}{R}\dfrac{1}{s+\dfrac{1}{RC}}]\)
\begin{eqnarray} =\frac{V}{R}\left(1-e^{-\frac{1}{RC}t}\right)\end{eqnarray}
ということで電流iの時間変化i(t)が求まったので、VrとVcも求まる。Vrは、Ri(t)なので、
\begin{eqnarray} Vr=V\left(1-e^{-\frac{1}{RC}t}\right)\end{eqnarray}
Vr+Vc=Vなので、Vc=V-Vr よって、
\begin{eqnarray} Vc=Ve^{-\frac{1}{RC}t}\end{eqnarray}
RC=τ（タウ）と置くと、この値の次元は、
\begin{eqnarray} 時定数{\tau}の次元&=&{\mathrm{[F]}}×{\mathrm{[Ω]}}\\ &=&\frac{{\mathrm{[A]}}{\mathrm{[s]}}}{{\mathrm{[V]}}}×\frac{{\mathrm{[V]}}}{{\mathrm{[A]}}}\\ &=&{{\mathrm{[s]}}}\tag{15} \end{eqnarray}
となり、見事に[s]つまり”秒”となる。普通の時間の単位ですね。たとえば、
R=3.3KΩかつC=1μFとすると、RCは3.3×103x1x10-6=3.3×10-3[s] つまり3.3msとなる。
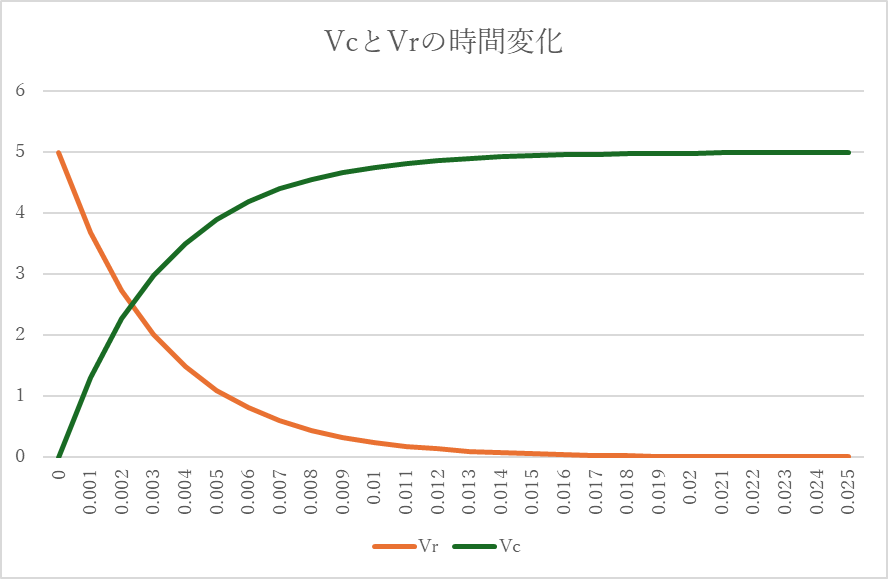
この時定数の時に、tを変化させたときのVrおよびVcの変化のグラフである。例によってExcelで描きました。時刻t=0の時からVcはゆっくりと上昇していくが、ちょうとt=RCな時刻では、電圧はV/eとなる。eの値は、以前の記事(マクローリン展開と近似 例1 自然対数の底eの近似値)で求めたように2.72程である。Vcを使って、電源が入った直後の電圧の上昇を遅らせることができるので、これを使って、Power-on Resetができる。ロジック回路への応用例を別記事で紹介しよう。
コメント