計測した信号の大きさを定量的にはかることは重要である。今、
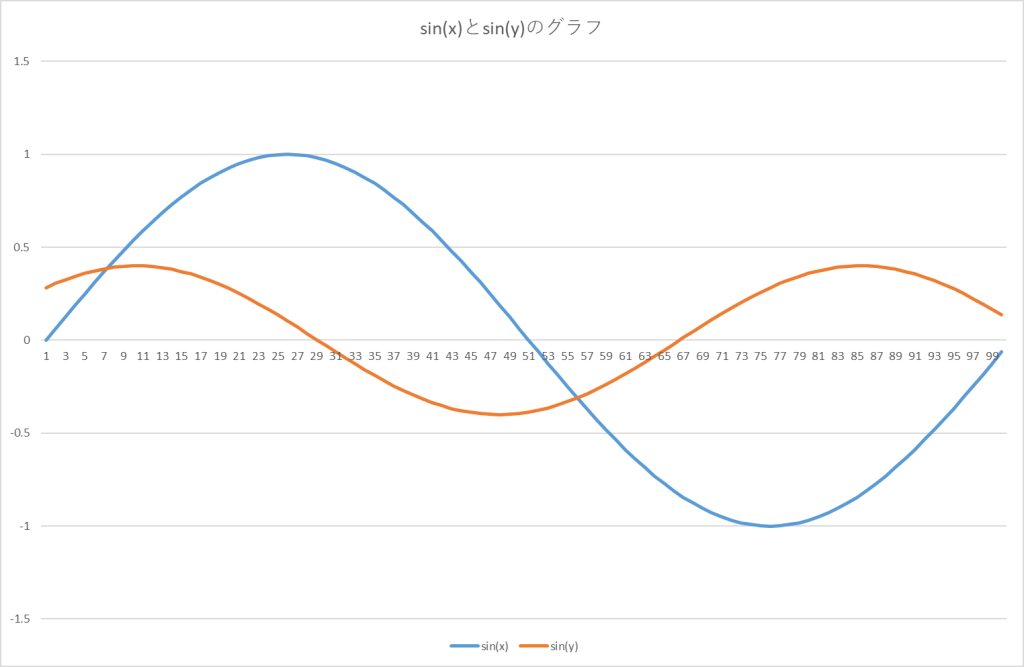
という二つの正弦波について、その振幅あるいは強さ(縦軸)を比較してみよう。一見して、オレンジ色のsin(y)なる波が、青色のsin(x)より”小さい”ことは見てとれる。それは定性的な記述であって、sin(y)はsin(x)の何分の1なのだろうか?それを計算したい。一つの方法は、”全振幅”で評価するやり方である。今の場合sin(x)の全振幅は2であるが、sin(y)の全振幅は正確な値が読み取れない。両方とも正負の値が交番するので普通の平均値はゼロである。sin(x)を抜き出すと、
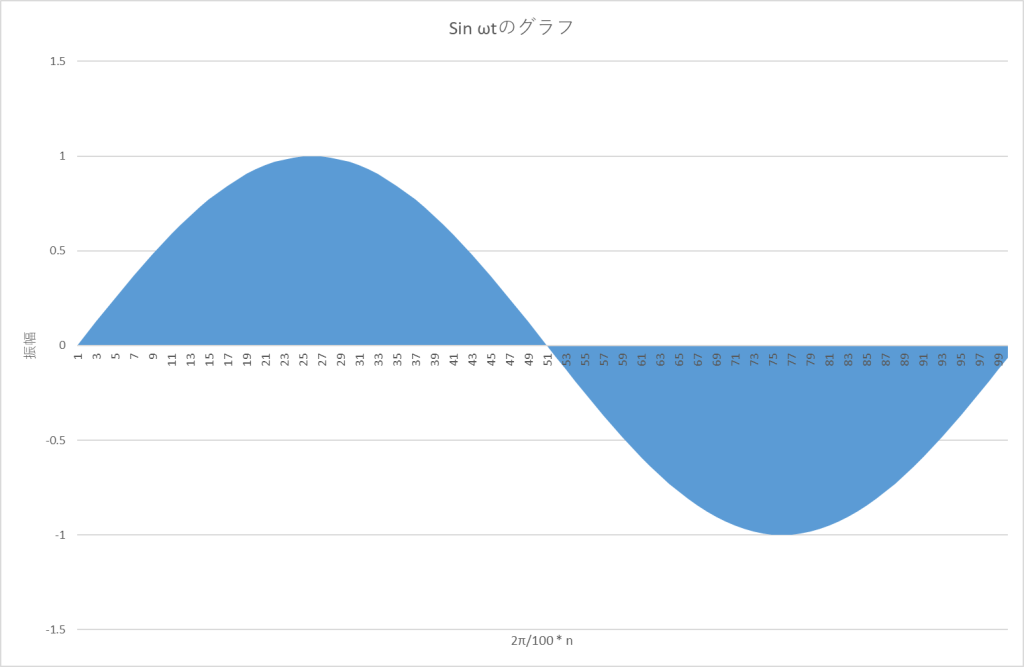
まず自乗する。
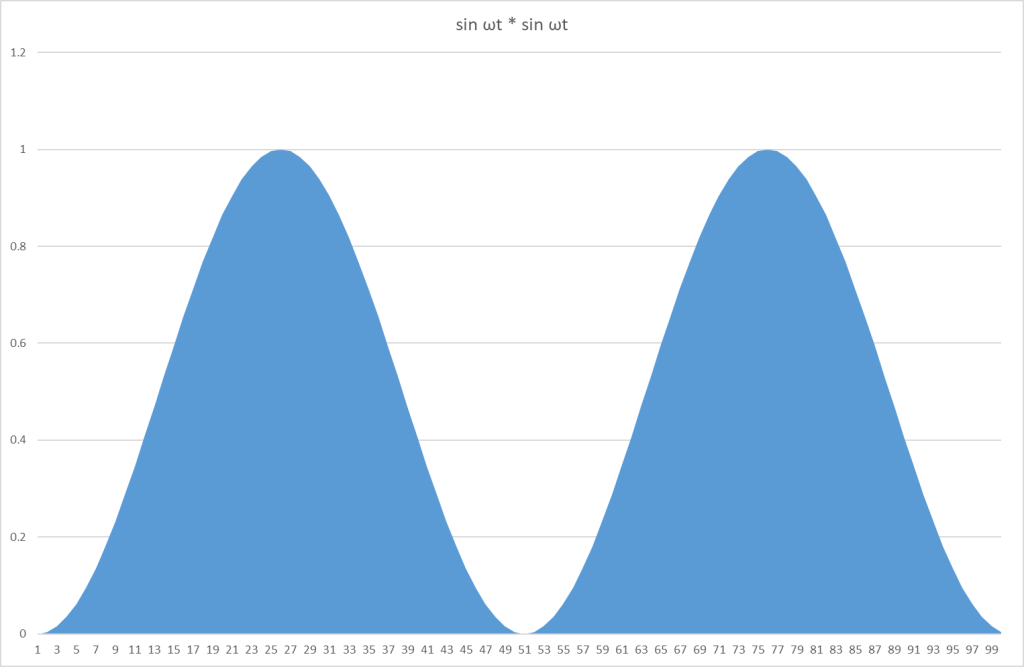
自乗(square)したのに正弦波に見えるが、これはいいのか?って、自乗したので、最大値は1で、全部+の値である。(自乗したので当然である)正弦波に見えるのも間違いではなく、
\(\cos 2\theta=\cos^2\theta-\sin^2\theta\)
という倍角の公式を思いついた人は勘が良いです。右辺に欲しい項(\(sin^2\theta\))があるよね。
今\(\cos^2\theta+\sin^2\theta=1\)なので、
\(\cos 2\theta=1-2\sin^2\theta\)
これを\(\sin^2\theta\)について解くと、
\(\sin^2\theta=\dfrac{1-\cos2\theta}{2}\)
\(=0.5-\dfrac{\cos2\theta}{2}\)
右辺第二項は、最小値が-0.5で、最大値が+0.5なので、結局周期が半分(つまり周波数2倍)で0.5だけ+側にシフトした正弦波(余弦波)なので、上のグラフで合っていますね。こいつの面積を求めたいわけです。面積を求めること=積分なので、数値的に積分できますが、今は波形が式で与えられているので、解析的に求めることができるでしょう。
全体の面積をSとすると、S/4(上図でx軸が0~24の範囲)を求めます。
\(\displaystyle\dfrac{S}{4}=\int_0^\dfrac{\pi}{2}\dfrac{1-\cos2x}{2}dx\)
\(=\dfrac{1}{2}\left[x+\dfrac{1}{2}\sin2x\right]^\dfrac{\pi}{2}_0\)
\(=\dfrac{\pi}{4}\)
したがって\(S=\pi\)です。
区間の幅は、0~\(2\pi\)なので、平均高さ、つまり矩形にならしたとするとその値は、面積を幅で割ればいいので、\(\dfrac{\pi}{2\pi}\)で、\(\dfrac{1}{2}\)、最初に自乗してますから次元を合わせるためにこの値の平方根を取って、\(\dfrac{1}{\sqrt2}\)が答えとなります。これがR.M.S値ということになります。有理化すると、その値は\(\dfrac{\sqrt2}{2}\)となり約0.707。最大値が1で計算していましたので、R.M.S値は0.707となります。これを実効値ともいいます。R.M.S.というのは、
実は、Root Mean Squareの略で、略語なので正式にはドット(.)を付けますが、付けない例もあるようです。Square(自乗ないし二乗)して、Mean(平均)を取り、最後にRoot(平方根)を取るという操作そのものを指しています。
実例で考えると、家庭用の交流100Vとは、電圧の最大値が100Vということではなく、実効値が100Vということです。つまり最大電圧は、その1.414倍の141Vくらいということですね。その関係をグラフで示すと、
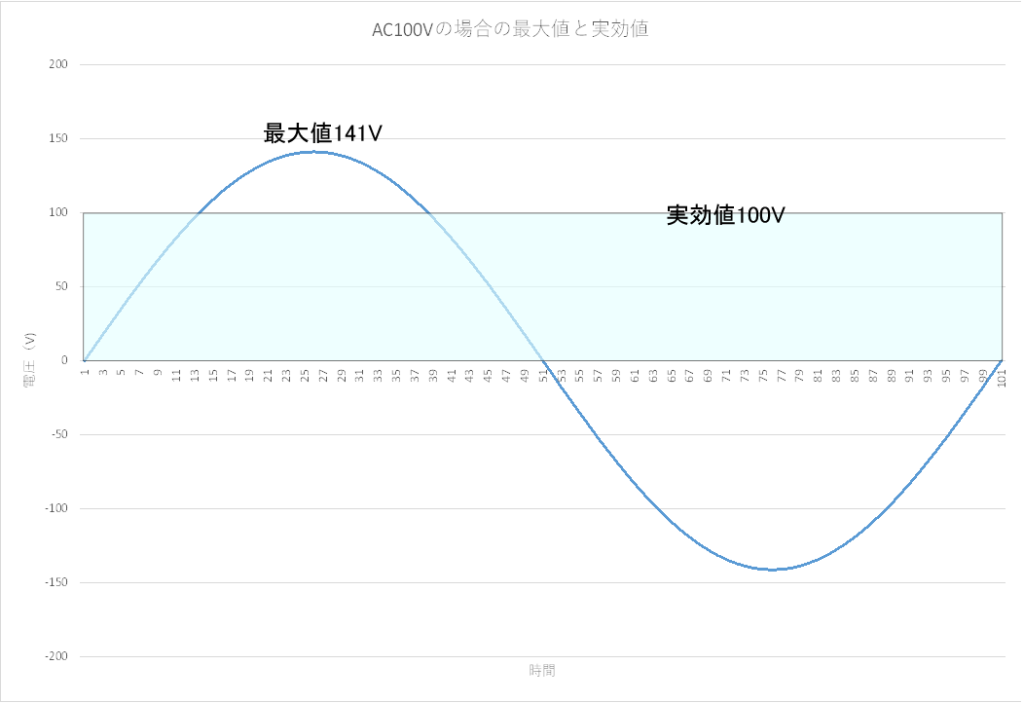
電圧がプラスマイナスを行ったり来たりしているので、平均的ないし効果的には100V相当というのが実効値の意味です。
以上が正弦波の場合でした。同様の計算によって、三角波の場合のR.M.S.値も求めることができます。
正弦波と三角波の関係は、
ということなので、当然ながら三角波の実効値は正弦波の場合よりは低くなるはずですが、実際の値を次回計算してみましょう。R.M.S.の逆を手順として適用すればいいので、正弦波と同様に自乗して、時間平均を取り、最後に平方根をとればいいわけです。



コメント
[…] 定積分の初級練習問題ですね。前記事から続く。 […]