グラフを使った憶え方
まず\(\sin x \)のグラフです(再掲)
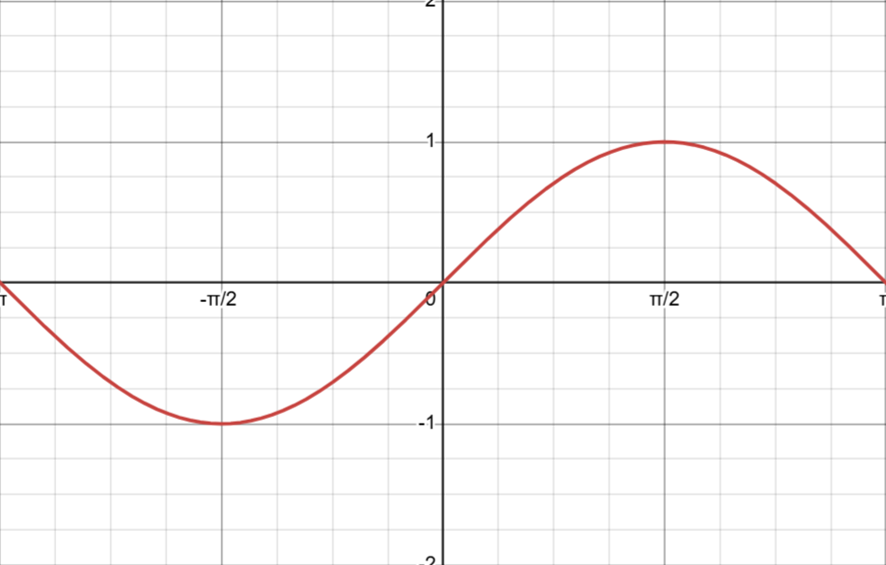
縦軸が\(\sin x\)で、横軸は\(x\)だとすると、\(\sin x\)の\(x\)に関する微分とは、グラフの傾き=接線の勾配に他ならないので、原点\(O\)付近でのグラフの傾きは、1である。それが最大値で、勾配は徐々に低下して、\(x = \dfrac{\pi}{2}\)で0になる。さらに低下し続けて、\(x = \pi\)で-1。なので、それをグラフに書くと、
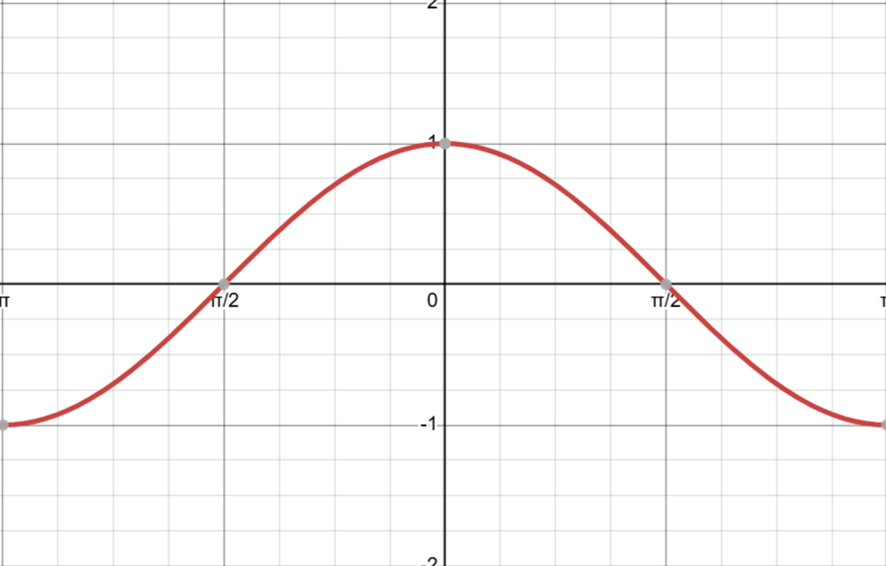
これって\(\cos x\)じゃないの。だから\(\sin x\)の微分は\(\cos x\)。上図の勾配は、原点で水平線つまり勾配0で、そこから徐々に低下(つまりマイナス領域)して\(x = \dfrac{\pi}{2}\)で、最小値-1となり、そこから増加に転じて\(x = \pi\)で再び0になる。グラフにすると、
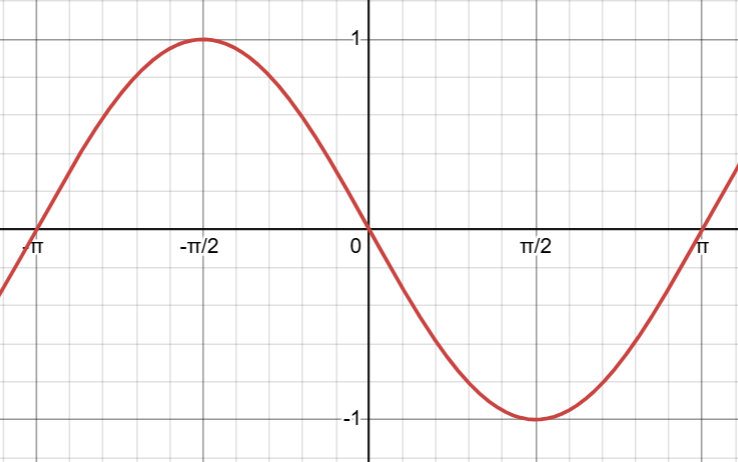
これは\(-\sin x\)である。従って\(\cos x\)の微分は\(-\sin x\)である。憶えやすいでしょ?



コメント