少しずつ三角関数\(\sin \thetaや\cos \theta\)について書いてます。
この記事では\(\sin ^2 \theta + \cos ^ 2 \theta = 1 \)を思い出して、どうやって証明するのだっけという経緯について述べます。まず三角関数の定義ですが、下図の直角三角形で、
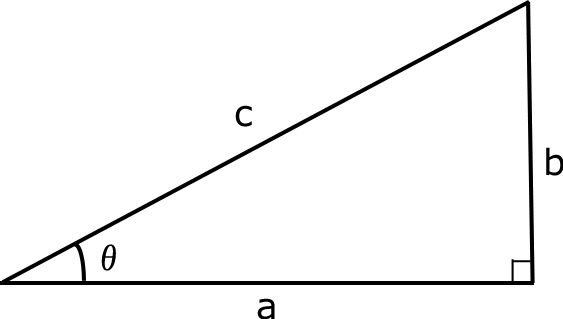
\(\cos \theta = \dfrac{a}{c}で\sin \theta = \dfrac{b}{c}\)
なので、\(\sin ^2 \theta + \cos ^ 2 \theta = (\dfrac{a}{c})^2 + (\dfrac{b}{c})^2 \)
右辺を整理すると、\(\dfrac{a^2+b^2}{c^2}\)でみたことあるような式で、ピタゴラスの定理により直角三角形の斜辺(直角に対する辺C)の自乗が残りの二辺(aとb)の自乗和に等しいということで、上図の直角三角形において、
\(a^2 + b^2 = c^2\)
なので右辺は結局1。
従って、\(\sin ^2 \theta + \cos ^ 2 \theta = 1 \)が証明された。って、ピタゴラスの定理の証明はどうするの?調べてみると多数のアプローチがあるようです。https://ja.wikipedia.org/wiki/%E3%83%94%E3%82%BF%E3%82%B4%E3%83%A9%E3%82%B9%E3%81%AE%E5%AE%9A%E7%90%86
ここに網羅されています。エレガントなものから、力ずく(巾級数展開で行く)のものまで多彩。微積分を使うのが面白いですかね。
ちなみに、\(\sin \thetaと\cos \theta\)を混同しやすいのですが、筆記体のSとかCとかの書き方の連想で憶えるやり方もあるらしいです。(昔学生さんに教えてもらいました)筆者は、\(\theta = 0 の時は、\cos \theta = 1 \sin \theta = 0 \)ということで、憶えます。それが太古からの習慣になってます。\(\theta = 0 ならば、\dfrac{a}{c}\)は1に漸近しますよね。つまり c = aになるのでこちらがcosです。以前の記事でsinとcosのグラフを示しましたが、まずそれを憶えるのが吉です。すくなくとも筆者にとってはね。グラフが頭にあれば、微分の結果もすぐに分かります。グラフさえ憶えられば……。



コメント